 |
 |
 |
    |
|
Maszyny proste
Maszyny proste
Maszyny proste to nieskomplikowane przedmioty używane tak, aby pracę mechaniczną (np. przy podnoszeniu przedmiotu) można było wykonać zmieniając zwrot lub\i wartość siły. Używane są jako narzędzia ułatwiające wykonywanie wszelakich prac. Są też elementami urządzeń mechanicznych i elektromechanicznych. Zasada działania tych przedmiotów oparta jest na zmniejszeniu naszej siły kosztem zwiększenia drogi pokonywanej przez przedmioty. Można też równoważyć duży ciężar mniejszym zawieszonym w odpowiedniej odległości od punktu podparcia ciała utrzymującego ciężary.
§ 1. Rodzaje maszyn prostych
- dźwignia jednostronna
- dźwignia dwustronna
- bloczek nieruchomy
- bloczek ruchomy
- dwukrążek
- wielokrążek
- wielokrążek potęgowy
- klin
- śruba
- prasa hydrauliczna
§ 2. Dźwignia jednostronna
Każdy chyba wie jak wygląda dźwignia jednostronna. Jej zasada działanie polega na tym, że jeśli jakiś ciężki przedmiot umieścimy blisko osi obrotu, to aby go podnieść, możemy zadziałać siłą o wiele razy mniejszą od ciężaru tego przedmiotu, jeśli zadziałamy wystarczająco daleko od osi obrotu. Jest to oczywiście przykładowe zastosowanie. A oto dźwignia jednostronna:
Warunek równowagi dla dźwigni jednostronnej
Trzeba dodać, ze warunek ten jest spełniony tylko wtedy gdy siły 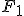 i i 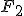 , działają w przeciwne strony (ściślej rzecz biorąc chodzi o momenty tych sił ( , działają w przeciwne strony (ściślej rzecz biorąc chodzi o momenty tych sił (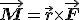 ), ale o tym w innym temacie). Myślę, że jest to dość łatwo pojąć, gdyż mamy z tym styczność na co dzień i jest to stosunkowo intuicyjne. Odległości ), ale o tym w innym temacie). Myślę, że jest to dość łatwo pojąć, gdyż mamy z tym styczność na co dzień i jest to stosunkowo intuicyjne. Odległości 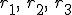 są odległościami punktów przyłożenia sił od osi obrotu. Siła Q jest przyłożona w środku ciężkości belki, który często jest środkiem geometrycznym belki (założenie o równomiernym rozkładzie masy w belce).
Ciekawą sprawą jest to, że możemy zupełnie dowolnie wybrać punkt na belce względem, którego obraca się belka, ale o tym za chwilę. są odległościami punktów przyłożenia sił od osi obrotu. Siła Q jest przyłożona w środku ciężkości belki, który często jest środkiem geometrycznym belki (założenie o równomiernym rozkładzie masy w belce).
Ciekawą sprawą jest to, że możemy zupełnie dowolnie wybrać punkt na belce względem, którego obraca się belka, ale o tym za chwilę.
§ 3. Dźwignia dwustronna
Zasada działania dźwigni dwustronnej jest bardzo podobna do zasady działania jej jednostronnej koleżanki. Z dźwignią tą mamy do czynienia np. na placu zabaw na popularnej dwuosobowej huśtawce. Wiadomo, że jeśli cięższa osoba kołysze się z lżejszą, to będzie jąprzeważać i nici z zabawy. Ale jeśli osoba cięższa przesunie się bliżej punktu podparcia a osoba lżejsza się jeszcze bardziej od niego odsunie to zabawa wre. A oto dźwignia dwustronna:
Warunek równowagi dla dźwigni dwustronnej: 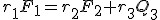 Jak widać, jest bardzo podobny do tego dla dźwigni dwustronnej. Wcześniej napisałem, że oś obrotu można sobie wyznaczać w dowolnych punktach od osi obrotu. Najlepiej widać to na przykładzie dźwigni dwustronnej. Wybierzmy sobie oś obrotu w środku ciężkości. Zatem odległość siły Q od osi obrotu wynosi 0, zatem tej siły nie trzeba brać pod uwagę. warunek dla takiej dźwigni będzie wyglądał następująco:
Jak widać, jest bardzo podobny do tego dla dźwigni dwustronnej. Wcześniej napisałem, że oś obrotu można sobie wyznaczać w dowolnych punktach od osi obrotu. Najlepiej widać to na przykładzie dźwigni dwustronnej. Wybierzmy sobie oś obrotu w środku ciężkości. Zatem odległość siły Q od osi obrotu wynosi 0, zatem tej siły nie trzeba brać pod uwagę. warunek dla takiej dźwigni będzie wyglądał następująco: 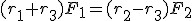 . Jest to bardzo użyteczna metoda, wtedy kiedy nie znamy masy belki.
Podstawowe informacje o bloczkach . Jest to bardzo użyteczna metoda, wtedy kiedy nie znamy masy belki.
Podstawowe informacje o bloczkach
Bloczek, zwany też krążkiem, to narzędzie często używane do podnoszenia jakichś dużych ciężarów w pionie. Pomagają nam one w tym, że my musimy działać tylko siłą, tzn nie musimy się przemieszczać. Możemy stać w miejscu i coś podnosić lub opuszczać.
Aby dobrze zrozumieć poniższe zależności trzeba znać jedną z podstawowych zasad: Jeżeli między bloczkiem a przerzuconą przez niego linką nie działają siły tarcia, to siły naciągu nici po obu stronach bloczka są takie same. Wynika to z III zasady dynamiki Newtona. Wiedzieć jeszcze trzeba, że jeśli nie uwzględniamy ruchu obrotowego bloczka, to masę krążka lub układu krążków przyjmuje się za zerową. Masę linek także się zaniedbuje. Poza tym, jeżeli przez blok przerzucimy linkę (a na jej końcach jakieś masy) i bloczek ten powiesimy na dynamometrze, to dynamometr wskaże siłę równą sumie dwóch sił naciągu: tej po jednej i tej po drugiej stronie bloczka (N1+N2). Jeśli między linką a bloczkiem nie występuje tarcie, to dynamometr wskaże 2N. Ponadto bardzo ważne jest częstokroć wykorzystywane założenie o nierozciągliwości linki. Istotnie, jest ono nieodzowne, ponieważ masy umieszczone na obu końcach takiej linki mogłyby wywoływać różne rozciągnięcia, a wskutek tego masy przebyłyby różne drogi i miałyby różne przyspieszenia. Komplikowałoby to sprawę, zatem w większości zagadnieniach przyjmuje się nierozciągliwość linki.
§ 4. Bloczek nieruchomy
Bloczek nieruchomy, ponieważ krążek ten może się tylko obracać, nie zaś poruszać ruchem postępowym. A oto bloczek nieruchomy:
Prawie zawsze zakłada się, ze tarcie między blokiem i linką nie występuje. To założenie jest zaznaczone na rysunku (siły naciągu N są równe po obu stronach).
Warunek równowagi dla bloczka nieruchomego: 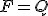 (na rysunku nie ma zaznaczonej siły Q, ale chyba każdy wie, gdzie jest ona przyłożona). Warunek ten wynika z tego, że aby masa pozostała w spoczynku lub poruszała się jednostajnie to góry siła naciągu musi równoważyć siłę Q. Wykorzystując III zasadę dynamiki: my działamy na linkę siłą F, to linka działa na nas siłą -F. Skoro linka jest naciągnięta siłą N to znaczy, że my także musimy zadziałać taką siłą. Zatem F=N=Q.
(na rysunku nie ma zaznaczonej siły Q, ale chyba każdy wie, gdzie jest ona przyłożona). Warunek ten wynika z tego, że aby masa pozostała w spoczynku lub poruszała się jednostajnie to góry siła naciągu musi równoważyć siłę Q. Wykorzystując III zasadę dynamiki: my działamy na linkę siłą F, to linka działa na nas siłą -F. Skoro linka jest naciągnięta siłą N to znaczy, że my także musimy zadziałać taką siłą. Zatem F=N=Q.
Przykład 1 - maszyna Atwooda
Maszyna Atwooda pokazana jest na rysunku poniżej. Znając masy ciężarków i przyspieszenie ziemskie, należy wyznaczyć przyspieszenie układu ciężarków i siłę naciągu nici.
Rozwiązanie:
Na rysunku od razu zaznaczyłem wszystkie siły oraz kierunek, w którym poruszają się obie masy. Rozpatrujemy bloczek idealnie gładki, zatem 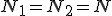 . Zadanie nie jest trudne. Wystarczy zapisać II zasadę dynamiki dla każdej z mas . Zadanie nie jest trudne. Wystarczy zapisać II zasadę dynamiki dla każdej z mas
Po dodaniu tego układu stronami, pozbywamy się siły naciągu, której nie znamy (właśnie dlatego to robimy)
Teraz można wyliczyć siłę naciągu, np. z równania Newtona dla masy 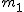 : :
Przykład 2 - maszyna Atwooda z tarciem linki o blok
Linka jest przewieszona przez nieobracający się bloczek i obciążona z obu stron odpowiednio
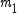 i i
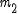 , ,
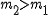 . Obliczyć przyspieszenie . Obliczyć przyspieszenie  i naciągi i naciągi 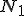 i i 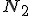 , jeśli siła tarcia o bloczek wynosi , jeśli siła tarcia o bloczek wynosi 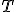 . Masę linki i bloczka zaniedbać.
Rozwiązanie: . Masę linki i bloczka zaniedbać.
Rozwiązanie:
Na rysunku zaznaczyłem wszystkie siły. Siła tarcia po każdej ze stron jest równa połowie całkowitej siły tarcia działającej pomiędzy linką i bloczkiem. Dzieje się tak dlatego, że siła nacisku rozkłada się równomiernie na każdej połówce bloczka. Siła N to siła naciągu, która występowałaby kiedy nie byłoby uwzględnianie tarcie. Siły naciągu z indeksami są siłami naciągu N pomniejszonymi lub powiększonymi o wartość T/2. Rysując siły tarcia kierowałem się zasadą, która mówi, że siła tarcia działa zawsze przeciwnie do kierunku ruchu ciała.
Można zatem przejść do pisania równań Newtona dla każdej z mas
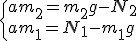 oraz jak widać z rysunku:
oraz jak widać z rysunku: 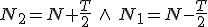 Dodając układ równań stronami mamy, że:
Dodając układ równań stronami mamy, że:
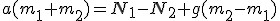 . Z równań obok widać, ze . Z równań obok widać, ze
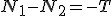
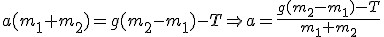 Korzystając z powyższych równań:
Korzystając z powyższych równań:
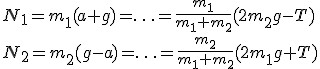
Przykład 3
Należy obliczyć przyspieszenie układu (rysunek) i policzyć siłę naciągu nici. Dane 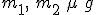 Rozwiązanie:
Rozwiązanie:
Wystarczy zapisać II zasadę dynamiki dla każdego ciężarka osobno. Siły zaznaczyłem wcześniej. Układ porusza się w prawo.
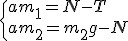 Wiemy, ze siła tarcia wynosi
Wiemy, ze siła tarcia wynosi 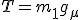 , zatem dodając równania stronami: , zatem dodając równania stronami:
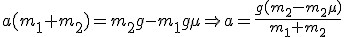
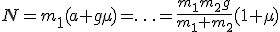
§ 5. Bloczek ruchomy
Bloczek ruchomy, ponieważ poza wykonywanym przez niego ruchem obrotowym, bloczek ten może się także poruszać ruchem postępowym. Oto bloczek ruchomy:
Warunek równowagi dla bloczka ruchomego: 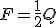 .
Warunek ten wynika z tego, że ciężarek o masie m jest utrzymywany przez dwie siły naciągu: Q=2N. Na takiej samej zasadzie jak dla bloczka nieruchomego wnioskujemy, że N=F, zatem .
Warunek ten wynika z tego, że ciężarek o masie m jest utrzymywany przez dwie siły naciągu: Q=2N. Na takiej samej zasadzie jak dla bloczka nieruchomego wnioskujemy, że N=F, zatem 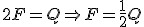 . Z tego wynika, że jeśli budowniczowie chcą przetransportować worek cementu z ziemi na dach, mogą użyć bloczka ruchomego, aby zmniejszyć siłę do tego potrzebną o połowę. . Z tego wynika, że jeśli budowniczowie chcą przetransportować worek cementu z ziemi na dach, mogą użyć bloczka ruchomego, aby zmniejszyć siłę do tego potrzebną o połowę.
Przykład 4
Dany jest układ dwóch bloczków: ruchomy i nieruchomy jak pokazuje rysunek. Znaleźć przyspieszenia mas 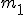 i i 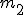 .
Rozwiązanie: .
Rozwiązanie:
Znów trzeba napisać równania dla każdej z mas, ale najpierw trzeba się upewnić czy przyspieszenia obu mas są takie same. Otóż nie są. Przyspieszenie masy 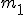 jest dwa razy mniejsze od przyspieszenia masy jest dwa razy mniejsze od przyspieszenia masy 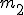 . Wynika to z tego, że masę . Wynika to z tego, że masę 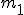 ograniczają dwie siły naciągu i podczas gdy masa ograniczają dwie siły naciągu i podczas gdy masa 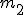 przebędzie drogę s to masa przebędzie drogę s to masa 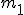 przebędzie drogę s/2. Jak wiadomo: przebędzie drogę s/2. Jak wiadomo: 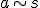 zatem zatem 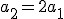 . Teraz można przejść do równań: . Teraz można przejść do równań:
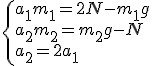 Po pomnożeniu drugiego równania przez 2 i dodaniu go do pierwszego otrzymujemy:
Po pomnożeniu drugiego równania przez 2 i dodaniu go do pierwszego otrzymujemy:
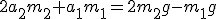 , Wiemy, że , Wiemy, że 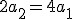 , zatem , zatem
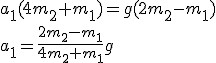 a więc
a więc 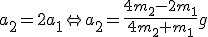
Przykład 5 - zadanie nr 5 z I etapu OF 2007
Rozważmy układ bloczków i mas przedstawiony na rysunku. Z jakim przyspieszeniem porusza się masa 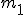 ? Liny są nieważkie, wiotkie i nierozciągliwe. Bloczki są nieważkie. Fragmenty lin nie znajdujące się na bloczkach pozostają stale proste. Pomiń tarcie i opór powietrza.
Rozwiązanie: ? Liny są nieważkie, wiotkie i nierozciągliwe. Bloczki są nieważkie. Fragmenty lin nie znajdujące się na bloczkach pozostają stale proste. Pomiń tarcie i opór powietrza.
Rozwiązanie:
Na rysunku zaznaczyłem wszystkie siły. Tutaj zapisanie równań Newtona za bardzo nic nie da (zatem typowo olimpijskie zadanie - odejście od standardów). Trzeba się zastanowić nad siłami naciągu.
1) Z braku tarcia pomiędzy linkami a bloczkami wynika, że
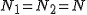 2) Siła N3 jest równa
2) Siła N3 jest równa  3) Z braki tarcia wynika, że
3) Z braki tarcia wynika, że 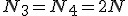 4) Oraz znów z braku tarcia:
4) Oraz znów z braku tarcia: 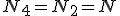 Dochodzi do równań:
Dochodzi do równań: 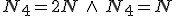 . Równanie to jest spełnione wtedy gdy . Równanie to jest spełnione wtedy gdy 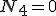 . Skoro . Skoro 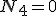 , to , to 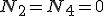 , zatem na bloczek najniżej opuszczony nie działają żadne siły naciągu więc masa , zatem na bloczek najniżej opuszczony nie działają żadne siły naciągu więc masa 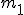 nie będzie przez nic ograniczana, czyli jej przyspieszenie nie będzie przez nic ograniczana, czyli jej przyspieszenie 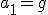
§ 6. Dwukrążek
Jak sama nazwa wskazuje dwukrążek jest złożony z dwóch bloczków: nieruchomego i ruchomego. Pokazuje to rysunek, na którym zaznaczyłem odpowiednie siły:
Warunek równowagi dla takiego układu krążków jest następujący: 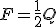 .
Łatwo można się domyślić, że .
Łatwo można się domyślić, że 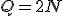 oraz z III zasady dynamiki oraz z III zasady dynamiki 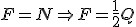
§ 7. Wielokrążek
Wielokrążek jest powieleniem dwukrążka. Rysunek przedstawia dwa równoważne schematy przedstawiające wielokrążek - tutaj dwukrążek podwójny:
Warunek równowagi dla takiego układu wynosi: 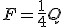 .
Podobnie jak wcześniej, ciężar jest unoszony przez 4 siły naciągu, a tak jak poprzednio F=N zatem Q=4F więc .
Podobnie jak wcześniej, ciężar jest unoszony przez 4 siły naciągu, a tak jak poprzednio F=N zatem Q=4F więc 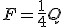 . Okazuje się, że dla układu k takich bloczków
Warunek równowagi dla wielokrążka: . Okazuje się, że dla układu k takich bloczków
Warunek równowagi dla wielokrążka: 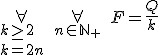
§ 8. Wielokrążek potęgowy
Jest to układ k bloczków ruchomych i jednego bloczka nieruchomego. Nazwa taka a nie inna, ponieważ jeżeli potraktujemy bloczek pierwszy jako podstawę potęgi, to następne bloczki ruchome będą się układać jak wykładniki potęg tej podstawy. Ma to też związek warunkiem równowagi dla takiego układu. Oto wielokrążek potęgowy:
Warunek równowagi dla takiego układu: 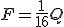 .
Wynika to z tego, że ciężar jest podtrzymywany za pomocą dwóch nici: Q=2N, a naciąg nici zmniejsza się co każdy bloczek dwa razy. Ogólny wzór dla wielokrążka potęgowego złożonego z k bloczków (łącznie z nieruchomym):
Warunek równowagi dla wielokrążka potęgowego: .
Wynika to z tego, że ciężar jest podtrzymywany za pomocą dwóch nici: Q=2N, a naciąg nici zmniejsza się co każdy bloczek dwa razy. Ogólny wzór dla wielokrążka potęgowego złożonego z k bloczków (łącznie z nieruchomym):
Warunek równowagi dla wielokrążka potęgowego: 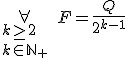
§ 9. Klin
Jak klin wygląda, to chyba każdy wie. Mimo wszystko przedstawię trochę bliżej klin, rozkład sił i jego przykłady w życiu codziennym. Oto klin w ujęciu fizycznym:
Jak widać, klin służy do przepoławiania czy też ćwiartowania różnych rzeczy. Takim klinem może być siekiera czy też nóż. Siłę z jaką rozpychane są części, na które kroimy jakiś materiał np. kawałek drewna można łatwo policzyć. Do tego sporządziłem schemat z rozkładem sił. Widać z niego, że 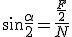 .
Zatem .
Zatem 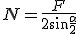 . Ze wzoru tego widać, że w przypadku noża . Ze wzoru tego widać, że w przypadku noża 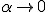 więc więc 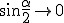 a z tego wynika, ze a z tego wynika, ze 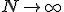 , więc im cieńszy nóż tym łatwiej nam kroić. Nawet z siekierze, klin nie ma dużego kąta łamiącego (na wzór pryzmatu), więc siła jaką działamy, nie musi być duża. W przypadku rzeczywistym: , więc im cieńszy nóż tym łatwiej nam kroić. Nawet z siekierze, klin nie ma dużego kąta łamiącego (na wzór pryzmatu), więc siła jaką działamy, nie musi być duża. W przypadku rzeczywistym: 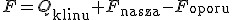
§ 10. Śruba
Śruby niestety nie umiem narysować. Zastosowanie i wygląd każdy chyba zna. Mogę tylko dodać, że z fizycznego punktu widzenia śruba to w przybliżeniu równani pochyła nawinięta na walec. Przyjmijmy, że znamy promień śruby, ciężar ciała i skok śruby, czyli odległość między jej kolejnymi progami. Wyobraźmy sobie, że do śruby mocujemy masę o ciężarze Q. Może nie jest to klasyczne zastosowanie, ale wyobraźmy sobie, że za pomocą tej śruby wyciągamy do góry ten ciężar. Praca przy wznoszeniu tego ciężaru może być obliczona na dwa sposoby: 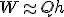 , gdzie h - to wspomniany skok śruby oraz , gdzie h - to wspomniany skok śruby oraz 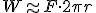 i z tego otrzymujemy, że i z tego otrzymujemy, że 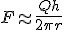
§ 11. Prasa hydrauliczna
Prasa hydrauliczna zwana też jest podnośnikiem hydraulicznym ze względu na jego zastosowanie. Jest często wykorzystywany w warsztatach samochodowych. Zasada działania jest oparta na prawie Pascala. Oto prasa hydrauliczna:
Warunek równowagi, a więc także wtedy masa jest podnoszona ruchem jednostajnym, jest następujący: 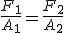 .
gdzie Ai to odpowiednie pole powierzchni tłoka. Jeśli, tak jak na rysunku, masa ma być podnoszona ruchem jednostajnym, to F2=Q, zatem siła jaką my musimy zadziałać F1 powinna wynosić: .
gdzie Ai to odpowiednie pole powierzchni tłoka. Jeśli, tak jak na rysunku, masa ma być podnoszona ruchem jednostajnym, to F2=Q, zatem siła jaką my musimy zadziałać F1 powinna wynosić: 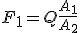 . Z zależności tej wynika, że aby podnieść ciężar Q ruchem jednostajnym do góry, to musimy naciskać na tłok z siła tyle razy mniejszą od ciężaru ciała ile razy powierzchnia tłoka, na którą naciskamy jest mniejsza od powierzchni ja jakiej spoczywa masa m. Pole powierzchni zmienia się kwadratowo wraz z liniowymi rozmiarami ciała, zatem wystarczy, że dwa razy zwiększymy powierzchnie tłoka, na którym ustawimy masę, a wtedy nasz siła maleje aż 4-krotnie. . Z zależności tej wynika, że aby podnieść ciężar Q ruchem jednostajnym do góry, to musimy naciskać na tłok z siła tyle razy mniejszą od ciężaru ciała ile razy powierzchnia tłoka, na którą naciskamy jest mniejsza od powierzchni ja jakiej spoczywa masa m. Pole powierzchni zmienia się kwadratowo wraz z liniowymi rozmiarami ciała, zatem wystarczy, że dwa razy zwiększymy powierzchnie tłoka, na którym ustawimy masę, a wtedy nasz siła maleje aż 4-krotnie.
|
 |
|
|