 |
 |
 |
    |
|
Opis ruchu w nieinercjalnych układach odniesienia
Opis ruchu w nieinercjalnych układach odniesienia
Jak już pisałem w działach: Transformacja Galileusza i Zasady dynamiki Newtona, zasady dynamiki obowiązują tylko w układach inercjalnych. Istnieją jeszcze układy nieinercjalne czyli takie, w których prawa fizyki swojej standardowej postaci. Okazuje się, że istnieje związek pomiędzy przyspieszeniami w układzie inercjalnym i nieinercjalnym.
Przyjmijmy, że wszystkie wielkości z 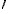 będą się odnosić do układu nieinercjalnego, a pozostałe (nieprimowane) do układu inercjalnego. Przypomnę, że układ nieinercjalny, to układ który obraca się lub/i porusza się z przyspieszeniem translacyjnym ( będą się odnosić do układu nieinercjalnego, a pozostałe (nieprimowane) do układu inercjalnego. Przypomnę, że układ nieinercjalny, to układ który obraca się lub/i porusza się z przyspieszeniem translacyjnym (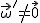 i i 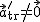 ), co na tym etapie trzeba przyjąć "na wiarę". ), co na tym etapie trzeba przyjąć "na wiarę".
§ 1. II zasada dynamiki w układzie nieinercjalnym
1.1. Postać matematyczna
Związek między siłami działającymi na ciało w układzie nieinercjalnym i inercjalnym jest następujący:
Powyższe siły maja swoje nazwy:
 - siła wypadkowa działająca na ciało w układzie nieinercjalnym, - siła wypadkowa działająca na ciało w układzie nieinercjalnym,
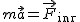 - siła wypadkowa działająca na ciało w układzie inercjalnym, - siła wypadkowa działająca na ciało w układzie inercjalnym,
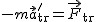 - siła translacyjna[1] (siła pozorna[2]), - siła translacyjna[1] (siła pozorna[2]),
 - siła Eulera (siła pozorna), - siła Eulera (siła pozorna),
 - siła Coriolisa (siła pozorna), - siła Coriolisa (siła pozorna),
 - siła odśrodkowa (siła pozorna).
Siłę Coriolisa i Eulera zazwyczaj się pomija, gdyż ma ona niewielki wpływ na ruch.Tutaj też tak postąpimy. II zasada dynamiki w obracającym się ze stałą prędkością kątową i przyspieszeniem translacyjnym ma postać:
II zasada dynamiki w układach nieinercjalnych - siła odśrodkowa (siła pozorna).
Siłę Coriolisa i Eulera zazwyczaj się pomija, gdyż ma ona niewielki wpływ na ruch.Tutaj też tak postąpimy. II zasada dynamiki w obracającym się ze stałą prędkością kątową i przyspieszeniem translacyjnym ma postać:
II zasada dynamiki w układach nieinercjalnych

Tę postać II zasady dynamiki w układach nieinercjalnych będziemy stosować dalej.
1.2. Przykład przyspieszającego pociągu
Wyobraźmy sobie dwóch obserwatorów. Niech obserwator A spoczywa na peronie a obserwator B jedzie w przyspieszającym pociągu. Wszelkie obroty można zaniedbać. Przyjmijmy, ze na beztarciowej podłodze w pociągu znajduje się skrzynia o masie m. Pociąg przyspiesza.
Obserwator A
Załóżmy, że obserwator A jest inercjalnym układem odniesienia. Przekonajmy się czy tak jest naprawdę. Względem obserwatora A na skrzynię nie działają żadne siły (prócz reakcji od podłoża i ciężkości, ale one się równoważą). Zatem jeśli pociąg przyspiesza, to skrzynia nie będąca pod działaniem żadnej siły powinna zostać w miejscu podczas gdy pociąg się przemieszcza. I tak się dzieje w rzeczywistości, więc układ A można uznać za układ inercjalny. W układzie A wygląda to tak jakby pociąg wyjechał spod skrzyni. Zatem w układzie obserwatora A, który jest sztywno związany z Ziemią, jest spełniona zasada bezwładności. Dowodzi to, że układy sztywno związane z Ziemią (a więc i Ziemię) można traktować jako układ inercjalny. Ponadto, w temacie o transformacji Galileusza udowodniłem, że każdy układ odniesienia poruszający się względem układy inercjalnego ze stałą prędkością po linii prostej, także można traktować jako układ inercjalny.
Obserwator B
Często mamy do czynienia z podobnymi sytuacjami w tramwajach, pociągach i autobusach więc nie trudno będzie sobie wyobrazić naszą sytuację z punktu obserwatora B. Względem obserwatora B, ciało przemieszcza się w kierunku przeciwnym do ruchu pociągu, zatem obserwator B stwierdza, że poza siłami ciężkości i reakcji od podłoża na ciało działa jeszcze jakaś inna siła powodująca przyspieszenie ciała. Zobaczmy czy zgadza się to z naszym wzorem: 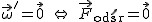 . Przyspieszenie pociągu to nasze przyspieszenie translacyjne . Przyspieszenie pociągu to nasze przyspieszenie translacyjne 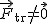 . Wypadkowa siła działająca w układzie inercjalnym . Wypadkowa siła działająca w układzie inercjalnym  , zatem , zatem  . Czyli rzeczywiście w układzie poruszającym się z przyspieszeniem na skrzynię działa dodatkowa siła, której pochodzenia nie znamy. Tak więc w istocie w układzie nieinercjalnym trzeba dodać dodatkowe siły, aby móc stosować II zasadę dynamiki. To dowodzi, że prawa fizyczne nie obowiązują w standardowej postaci w układach nieinercjalnych. . Czyli rzeczywiście w układzie poruszającym się z przyspieszeniem na skrzynię działa dodatkowa siła, której pochodzenia nie znamy. Tak więc w istocie w układzie nieinercjalnym trzeba dodać dodatkowe siły, aby móc stosować II zasadę dynamiki. To dowodzi, że prawa fizyczne nie obowiązują w standardowej postaci w układach nieinercjalnych.
Przykład 1
W wagonie, który porusza się z przyspieszeniem 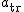 po prostym torze poziomym znajduje się równia pochyła nachylona pod kątem po prostym torze poziomym znajduje się równia pochyła nachylona pod kątem  do poziomu. Na równi leży ciało o masie do poziomu. Na równi leży ciało o masie 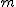 .
a) jakie powinno być przyspieszenie .
a) jakie powinno być przyspieszenie  wagonu, aby ciało nie zsuwało się z równi, jeżeli nie ma siły tarcia?
b) Jaką siłą nacisku wagonu, aby ciało nie zsuwało się z równi, jeżeli nie ma siły tarcia?
b) Jaką siłą nacisku 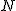 działa ciało na równię?
Rozwiązanie:
a)
Zadanie rozwiążę w nieinercjalnym układzie odniesienia związanym z wagonem czego można się było spodziewać. Tutaj układ odniesienia porusza się z przyspieszeniem atr i nie wykonuje obrotów więc nasz wzór uprości się do postaci: działa ciało na równię?
Rozwiązanie:
a)
Zadanie rozwiążę w nieinercjalnym układzie odniesienia związanym z wagonem czego można się było spodziewać. Tutaj układ odniesienia porusza się z przyspieszeniem atr i nie wykonuje obrotów więc nasz wzór uprości się do postaci:  . Zauważmy, że sytuacja statyczna może mieć miejsce wtedy kiedy siła translacyjna dociska ciało do równi pochyłej jak pokazuje to rysunek: . Zauważmy, że sytuacja statyczna może mieć miejsce wtedy kiedy siła translacyjna dociska ciało do równi pochyłej jak pokazuje to rysunek:
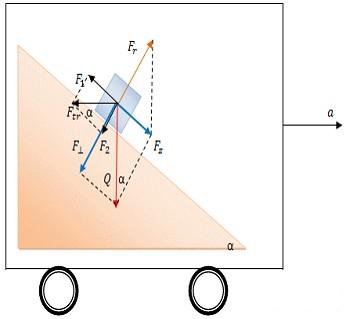
Rozłożyłem siłę translacyjną na składowe oraz zaznaczyłem odpowiednie kąty. Aby ciało pozostało nieruchomo na równi pochyłej, to siła wypadkowa w układzie inercjalnym musi być równa zeru co prowadzi do warunku (patrz rysunek): 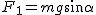 . Człon po prawej stronie to wypadkowa siła działających na ciało w układzie inercjalnym a człon po lewej stronie równania to składowa siły translacyjnej odpowiedzialna za ruch ciała wzdłuż powierzchni równi . Człon po prawej stronie to wypadkowa siła działających na ciało w układzie inercjalnym a człon po lewej stronie równania to składowa siły translacyjnej odpowiedzialna za ruch ciała wzdłuż powierzchni równi 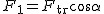 . A także siła translacyjna wyraża się wzorem (wartości ( . A także siła translacyjna wyraża się wzorem (wartości (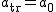 )) . )) .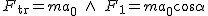 . Co po porównaniu daje . Co po porównaniu daje 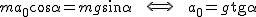 .
b)
Jak pokazuje rysunek do siły .
b)
Jak pokazuje rysunek do siły  trzeba dodać siłę trzeba dodać siłę 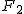 aby otrzymać siłę nacisku. Bez problemów można zauważyć, że aby otrzymać siłę nacisku. Bez problemów można zauważyć, że 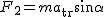 oraz oraz 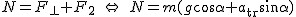 . .
[1] Z nazwą siła translacyjna nigdzie się nie spotkałem, ale w dalszej części będę właśnie tak nazywał ten rodzaj psuedosiły.
[2] Pojęcie siły translacyjnej, Coriolisa i bezwładności występuje tylko w układach nieinercjalnych. Poza tymi układami nie można posługiwać się tymi siłami, gdyż nie mają one swojego źródła (innego ciała) dlatego nie są siłami rzeczywistymi.
|
 |
|
|