Omówiliśmy już zasadę zachowania energii mechanicznej. Jest to zasada, która mówi o pewnej wielkości [energii], która jest niezależna od czasu, i która jest skalarem. Wiemy zatem, że energia jako wielkość liczbowa zostaje zachowana. Niestety nie pozwala ona w pełni opisać otaczającego nas świata, gdyż mamy informację jedynie o wielkościach skalarnych. My, żyjemy w przestrzeni, gdzie ruch pewnego obiektu (tutaj: punktu materialnego) jest opisywany przez wektory (np. kierunek ruchu). Przykładowo, za pomocą ZZE możemy określić jedynie szybkość końcową danego obiektu w pewnym rzucie, a nie da się określić prędkości, która dodatkowo posiada kierunek, zwrot, punkt zaczepienia. W takich sytuacjach z pomocą przychodzi zasada zachowania pędu (ZZP). Jest to prawo zachowania opisane w formie wektorowej. Można powiedzieć, że zasada zachowania pędu i energii wzajemnie się uzupełniają. Świetnym przykładem na potwierdzenia tego splotu są zderzenia, rozpady oraz zjawiska odrzutu. To dzięki ZZP-u odkryto, że poza elektronem i protonem neutron rozpada się także na antyneutrino elektronowe (rozpad beta minus).

Pęd jest wielkością wektorową. Ma określony kierunek zwrot i wartość. Na wstępie trzeba zaznaczyć, że pęd mechaniczny nie jest jedynym rodzajem pędu. Szerzej mówi o tym mechanika kwantowa. Pęd pojedynczego ciała o masie poruszającego się z prędkością 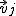jest zdefiniowany jako

Definicja pędu mechanicznego

W mechanice klasycznej istnieje ścisły związek pomiędzy pędem ciała z siłą nań działającą. W mechanice klasycznej na ogół więc . Podzielmy wszystko przez ; otrzymamy

Przy przejściu do granicy uzyskamy



Związek siły z pędem ciała (szkoła średnia)

Można to wyrazić w ścisłej postaci

Związek siły z pędem ciała

to suma wszystkich sił zewnętrznych działających na dane ciało.
Podany wyżej związek jest nazywany uogólnioną II zasadą dynamiki Newtona, ponieważ został wprowadzony do niej nowy człon

Uogólnienie polega wprowadzeniu do równania Newtona pojęcia zmienności masy. Takie uogólnienie jest przydatne szczególnie w kursie mechaniki relatywistycznej. W mechanice klasycznej niemal zawsze masa układu jest stała i tego będziemy się tutaj trzymać.

Na koniec tego punktu zdefiniujemy nową wielkość fizyczną zwaną popędem ciała z racji tego, że nieraz ten termin jest używany w literaturze. Popęd ciała jest zdefiniowany jako

Definicja popędu ciała (szkoła średnia)



Definicja popędu ciała

Zasada zachowania pędu

Jeżeli całkowita siła zewnętrzna działająca na układ cząstek jest równa zeru, to całkowity pęd układu jest stały.
Dowód:
Jeśli rozpatrzymy wszystkie siły działające na układ 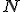ciał to będzie to suma sił wewnętrznych i zewnętrznych działających na dane ciało. Siły zewnętrzne oznaczę jako , a siły wewnętrzne jako . Ogólnie to siła wewnętrzna jaką ciało i-te działa na ciało j-ote.

Na samym początku dla łatwości zrozumienia poniższego dowodu proponują zapoznać się z dowodem dla cząstek.

Ciało 1 działa na ciało 2 i na ciało 3.
Ciało 2 działa na ciało 1 i na ciało 3
Ciało 3 działa na ciało i i na ciało 2

Dodając wszystkie równania stronami otrzymujemy

Uogólniając,

, ponieważ punkt materialny nie może działać sam na siebie siłą.

Tutaj skorzystałem z tego, że kolejność wskaźników nie ma znaczenia przy sumowaniu.

I na mocy III ZD pierwszy człon znika , zatem:

Jeśli siły zewnętrzna znikają to:

co stanowi treść zasady zachowania pędu. c.n.d.

3.1. Parametr zderzenia
Parametrem zderzenia nazywamy odległość prostej po jakiej porusza się środek masy jednego ciała od lini po jakiej porusza się środek masy drugiej kuli.
Rozpatrzmy dwie kuliste kule o promieniach i . Aby zaszło zderzenie parametr zderzenia musi spełniać warunek (konieczny, ale niewystarczający do tego, aby zaszło zderzenie)

Aby zderzenie zaszło na pewno, kule muszą znajdować się w tym samym czasie mniej więcej w tym samym miejscu, tzn. ich środki mas nie mogą znajdować się w odległości większej niż .

3.2. Zderzenia idealnie sprężyste
Zderzenia idealnie sprężyste, to zderzenia, w których w stanie końcowym mamy te same obiekty co przez zderzeniem i energie kinetyczna jest zachowania.
W tym rodzaju zderzeń zachowane jest zasada zachowania pędu oraz zachowana zostaje energia kinetyczna.
Przykładami zderzeń idealnie sprężystych są zderzenia cząsteczek gazy doskonałego, zderzenia elektronów, zderzenia kul bilardowych.

3.2.1. Zderzenia centralne
To zderzenia, w których parametr zderzenia jest równy 0.

3.2.2. Zderzenia niecentralne
To zderzenia, w których parametr zderzenia jest różny od 0.

3.3.3. Analiza zderzeń centralnych
Jeśli mamy dwa ciała o masach i oraz prędkościach przed zderzeniem , oraz po zderzeniu , , to możemy znaleźć związek między oraz , . Obowiązuje ZZP i ZZE:

Rozwiązaniem tego układu równań są:

3.3.4. Analiza zderzeń niecentralnych
Pełna analiza zderzeń niecentralnych, choć nie wymaga bardzo zaawansowanych narzędzi matematycznych (iloczyn wektorowy, równanie wektorowe prostej), to jest dość skomplikowana i zajmę się tą analizą tylko po części w przykładach. 

Przykład 1 - o zderzeniu centralnym, idealnie sprężystym ze ścianą
Punkt materialny o prędkości i masie leci wprost na ścianę i zderza się z nią idealnie sprężyście. Znaleźć zmianę pędu punktu materialnego po zderzeniu.

Rozwiązanie:
W każdym z zadań dotyczących zderzeń należy zapisać zasadę zachowania pędu i energii. Skupmy się na zasadzie zachowania pędu. Ważne jest, aby nie zapomnieć o tym, że pęd jest wektorem.
Pęd punktu materialnego przed zderzeniem można zapisać jako: . Gdzie to chwila, w której włączamy stoper, a to chwila zderzenia. Po cichu założyłem, że pierwotny zwrot prędkości w wybranym układzie współrzędnych jest dodatni.
Skoro punkt materialny (dalej PM) zderza się centralnie (wykorzystany pierwszą informację z zadania - "centralność" zderzenia), to wraca po tej samej prostej, po której pierwotnie się poruszało. To, że zderzenie jest idealnie sprężyste gwarantuje nam zachowanie energii, czyli to, że PM nie straci na szybkości. Mogłoby się wydawać, że zapomniałem o pędzie ściany, jednakże jego szybkość w porównaniu z szybkością PM jest zaniedbywalnie mała, zatem 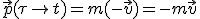, gdyż po zderzeniu PM zmienia zwrot lotu, zatem

Wzór ten stosuje się m.in. przy wyprowadzeniu wzoru na ciśnienia gazu w naczyniu zamkniętym.

Przykład 2 - o zderzeniu centralnym, idealnie niesprężystym
Ciało o masie i prędkości zderza się idealnie niesprężyście z ciałem o masie i prędkości . Znaleźć prędkości ciał po zderzeniu.

Rozwiązanie:
Zderzenie idealnie niesprężyste, to rodzaj zderzenia, w którym energia mechaniczna nie jest zachowana, gdyż część energii wskutek zderzenia zostaje zamieniona na ciepło, dźwięk, odkształcenie. Ciała po zderzeniu zlepiają się i pędzą, w jednym kierunku z jednakową prędkością . Możemy zapisać ZZP:

W szczególności, gdy ciało drugie przed zderzeniem stoi nieruchomo:

Prędkość jest zawsze skierowana zgodnie z . Ostatni wzór wykorzystuje się m.in. w analizie wypadów drogowych: za jego pomocą można określić szybkość samochodu, który "wbił" się w samochód stojący, np. na światłach. Szybkość znajduje się np. na podstawie śladów pozostawionych przez samochody.

Przykład 3 - o zderzeniu niecentralnym, idealnie sprężystym
Dwie kule o tej samej masie i prędkościach i zderzają się niecentralnie i idealnie sprężyście. Obliczyć kąt jaki tworzą prędkości kul po zderzeniu.

Rozwiązanie:
Zapisujemy zasadę zachowania pędu i energii:

Po podniesieniu pierwszego równania stronami:

Ten warunek jest spełniony tylko wtedy kiedy: , czyli .

Przykład 4 - o rakiecie wyrzucającej masę
Jednym z zastosowań zasady zachowania pędu jest napęd rakietowy, Napęd ten ten jest rozwiązaniem problemu, jak wprawić w ruch ciało bez bodźca zewnętrznego. Zasada działania silnika rakietowego polega na zwiększeniu pędu rakiety, które jest implikowane zmniejszeniem jej masy, poprzez wyrzuty gazu z silnika z szybkością względem rakiety, gdzie (prędkość rakiety jest przeciwnie skierowana do kierunku lotu rakiety). Niech masa rakiety w chwili wynosi 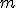. W tym momencie układ rakieta-gaz (dalej RG) ma pęd liczony względem Ziemi:

A po czasie , gdzie

gdyż wszystko odbywa się w układzie odniesienia Ziemi a nie rakiety.

Wielkości typu traktuje się jako mniejsze od innych (wielkości małe drugiego rzędu) i pomija się je. Tym samym to uczyniłem.

Rozpatrzmy przypadki
A)
B)

A)

Wyraz po lewej stronie jest siłą z II zasady dynamiki. Wyraz po prawej stronie nazywany jest siłą ciągu.

Powracając od przedostatniego równania, można zapisać:

(Zwracam uwagę na zniknięcie znaku -. Proszę zobaczyć na argument logarytmu i porównać z granicami całkowania w ostatniej całce)

gdzie jest masą rakiety wraz z gazem, a to masa rakiety bez gazu (z samym ładunkiem użytecznym), , gdzie jest masą wyrzuconego gazu. Zatem

Jak widać, przyrost prędkości zależy od stosunku . Im jest on większy, tym przyrost prędkości jest większy ( jest rosnąca).

B)

Tutaj już nie mogę pominąć zapisu wektorowego:

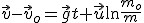(Ponownie zwracam uwagę na zniknięcie znaku -. Proszę zobaczyć na argument logarytmu i porównać z granicami całkowania w ostatniej całce)

Zatem zmiana prędkości jest zwiększona o czynnik gt w stosunku do poprzedniego przypadku.