 |
 |
 |
    |
|
Pojęcie siły tarcia
Siła tarcia jest jedną z najważniejszych sił w przyrodzie. Dzięki niej możemy chodzić, trzymać kredę i pisać nią po tablicy. Zatem siła tarcia jest nam pomocna, ale także staramy się ograniczyć jej wpływ w wielu przypadkach. Np. tarcie jest niepożądane w silnikach gdzie powoduje ich szybsze zużycie. Dlatego stosujemy smary, oleje, które wnikają w niedoskonałości powierzchni trących. § 1. Geneza siły tarcia
Z czego wynika siła tarcia? Tutaj nikt jeszcze nie podał w pełni uznanej przyczyny powstawania siły tarcia, jednakże powstało kilka teorii na ten temat, które wydają się być poprawne i we właściwy a przede wszystkim zgodny z doświadczeniem opisują zjawisko tarcia. Otóż, aby wyjaśnić ten proces trzeba przejść do mikroskopowego opisu budowy materii. My widzimy tylko to co makroskopowe i dlatego często wydaje nam się, że powierzchnie które dotykamy są idealnie gładkie. W rzeczywistości tak nie jest. Nawet lód czy powierzchnia lustra pod mikroskopem stają się szorstkie a ich "linia brzegowa" bardzo nieregularna i rozbudowana. Powstają ostro zakończone szczyty i garby, co powoduje wzrost lokalnego ciśnienia i powstaje ciśnieniowe zespolenie powierzchni zwane też przyleganiem powierzchni, czy też spawaniem na zimno. Jest to spowodowane tym, że cząsteczki ciał trących są na tyle blisko siebie, że mogą oddziaływać siłami międzycząsteczkowymi. Gdy próbujemy przesunąć jakieś ciała względem siebie, to natrafiamy na opór - siłę tarcia, której przezwyciężenie polega na rozerwaniu maleńkich spoiw, czyli połączonych fragmentów trących o siebie ciał, które powstały w ciśnieniowym zespoleniu powierzchni. 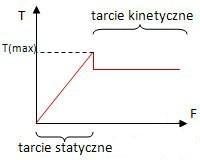Wykres przedstawia zależność siły tarcia od siły z jaką działamy na ciało:  § 2. Rodzaje sił tarcia
2.1. Wstęp Gdy próbujemy przesunąć jakieś ciało, działamy jakąś siłą F, ale nie udaje nam się ruszyć ciała z miejsca. Przeszkadza nam w tym siła tarcia statycznego, która występuje kiedy powierzchnie trące nie kiedy przesuwają się względem siebie. Kiedy zadziałamy siłą większą od F i ciało dalej nie ruszy z miejsca to znaczy, że siła tarcia statycznego także wzrosła. Zatem można dojść do wniosku, że siła tarcia działa kiedy my działamy i rośnie od 0 do wartości 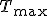 , czyli takiej kiedy ciało zaczyna się poruszać. Jak pokazuje życiowe doświadczenie, łatwiej jest pchać coś co jest już w ruchu niż wprawić to samo ciało w ruch. Okazuje się, że siła tarcia kinetycznego, czyli takiego kiedy powierzchnie trące przesuwają się względem siebie, jest nieco mniejsza od siły  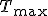i gdy ciągniemy lub pchamy jakieś ciało musimy działać siłą trochę mniejszą od tej jaką musieliśmy osiągnąć, aby wprawić ciało w ruch. 2.2. 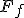Wartości sił tarcia i współczynniki tarcia  od angielskiego friction force - siła tarcia. 2.2.1. Tarcie statyczne Wartość siły tarcia statycznego
 2.2.2. Tarcie kinetyczne Wartość siły tarcia kinetycznego
 2.2.3. Współczynniki tarcia Współczynnik tarcia jest zazwyczaj mniejszy od jedności i bezwymiarowy. Zależność miedzy współczynnikami tarcia
 Współczynnik tarcia jest stałą, współczynnikiem proporcjonalności jeśli ktoś woli tak. Wartość współczynnika tarcia zależy od: rodzaju materiału, temperatury, obróbki powierzchni trących, zanieczyszczenia powierzchni. Trzeba zwrócić uwagę, że w próżni trudniej jest przesunąć ciało aniżeli na powietrzu. Nie ma tam żadnych cząsteczek powietrza przez co między powierzchniami tworzy się podciśnienie, które zwiększa silę nacisku, a zatem i siłę tarcia. W ośrodku takim jak powietrze, cząsteczki gazu wpychają się pomiędzy powierzchnie i pozwalają im "płynąć" po sobie. § 3. Cechy siły tarcia
Przykład 1 Samochód rozpędził się do prędkości 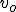 . Przed sobą zobaczył przeszkodę w postaci ściany i zaczął hamować. Współczynnik tarcia wynosi  a przyspieszenie ziemskie 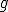 . Po przebyciu jakiej drogi samochód zatrzyma się? Rozwiązanie: (I) Z równań kinematycznych Niewątpliwie mamy do czynienia z ruchem jednostajnie opóźnionym, gdyż siła tarcia ma stałą wartość, a tylko ta siła działa na samochód podczas hamowania, więc to ona nadaje opóźnienie autu. W temacie Ruchy prostoliniowe został wyprowadzony związek  Prędkość końcowa 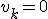 , ponieważ ciało zatrzyma się. Jedyną siłą nadającą opóźnienie ciału jest siła tarcia, zatem jest ona siłą wypadkową   (II) Z twierdzenia o pracy i energii kinetycznej Twierdzenie to mówi, że praca siły wypadkowej jest równa zmianie energii kinetycznej ciała nad jakim została wykonana praca. Można zapisać  Siła tarcia jest bez wątpienia siłą zewnętrzną zatem będziemy liczyć pracę tej siły (zresztą jest ona jedyną siła działającą na samochód). Zmiana energii kinetycznej jest związana ze zmianą prędkości samochodu. Prędkość ta zmienia się od 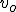 do 0. Zatem "delta" oznacza tyle co od końca odjąć początek, więc  Wiadomo, ze siła tarcia działa przeciwnie do kierunku ruchu ciała, zatem z definicji pracy widzimy, ze praca siły tarcia to  Powracając do przytoczonego twierdzenia   Teraz pozostaje się zastanowić o jaki współczynnik tarcia chodzi: kinetycznego czy może statycznego? Chodzi o współczynnik tarcia statycznego, ponieważ koło samochodu nie trze o powierzchni drogi, nie następuje przesuwanie się opony względem nawierzchni (boksowanie). Chwilowy punkt stuku nie przemieszcza się względem asfaltu, zatem autorowi zadania chodziło o współczynnik tarcia statycznego. Przykład 2 Do sań o masie 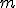 przyłożono siłę  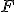pod kątem  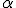, ale za każdym razem inaczej jak pokazuje rysunek. Z jakim przyspieszeniem poruszają się sanie, jeżeli współczynnik tarcia wynosi  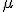? Rozwiązanie:  Rozpatrujemy sytuację pierwszą z lewej kierując się rysunkiem. Siłę należy rozłożyć na składową pionową i poziomą (wzdłuż osi Oy i Ox)  Siła tarcia jest skierowana przeciwnie do siły 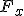 . Należy znaleźć siłę tarcia. Zadanie polega tak naprawdę na znalezieniu siły nacisku. Siły działające na sanie to  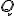i 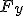 . Ta druga siła jest skierowana przeciwnie do Q, zatem siła wypadkowa w kierunku pionowym wynosi  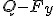. Taką siłą naciskają sanie na podłoże, zatem  . Ciało porusza się tylko w poziomie    W drugim przypadku siła 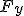 działa w tę samą stronę co Q, a więc zwiększa nacisk    Zatem w pierwszym przypadku uzyskamy większe przyspieszenie. 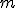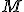Przykład 3 Jaką siłę  należy przyłożyć do masy  , w układzie przedstawionym na rysunku, aby poruszała się ona z przyspieszeniem  , jeżeli siła tarcia działa tylko między masą  i  , a współczynnik tarcia wynosi  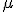? Rozwiązanie:  Tutaj już bez żadnych niespodzianek: równania Newtona dla każdej z mas  Dodając dwa pierwsze układy równań   |
 |
, gdzie ľ może oznaczać bezwymiarowy współczynnik tarcia statycznego lub kinetycznego (dynamicznego, posuwistego) a N siłę nacisku.