 |
 |
 |
    |
|
Równia pochyła
Równia pochyła
Równia pochyła jest jedną z maszyn prostych, ale ze względu na jej duże znaczenie w problemach fizycznych zdecydowałem się wyróżnić ten przyrząd w osobnym temacie.
Równia pochyła to po prostu płaska powierzchni nachylona pod kątem do poziomu, po której przesuwa się jakieś ciało czy to w górę czy też w dół.
§ 1. Równia pochyła bez tarcia
1.1. Rozkład sił na równi pochyłej bez tarcia
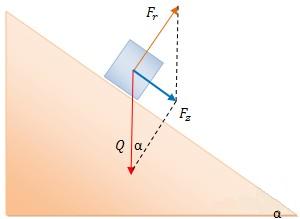 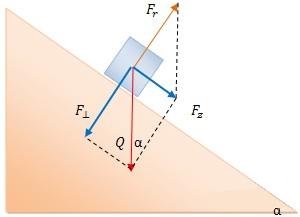
Aby opisać ruch ciała po równi pochyłej trzeba dobrze wiedzieć, które siły trzeba rozpatrzyć. Na ciało na równi pochyłej działają tylko dwie siły: ciężkości i reakcji od powierzchni równi. Siłą wypadkową tych dwóch siła jest tzw. siła zsuwająca 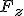 (rys. pierwszy z lewej). Wartość tej siły można obliczyć analizując rysunek: (rys. pierwszy z lewej). Wartość tej siły można obliczyć analizując rysunek: 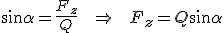 . Ten sam wynik można uzyskać rozkładając ciężar na dwie składowe (drugi rysunek): . Ten sam wynik można uzyskać rozkładając ciężar na dwie składowe (drugi rysunek): 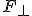 i i 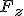 . Należy pamiętać, że gdy rozłożymy ciężar na dwie składowe to nie zajmujemy się już siłą Q, bo ona nas już nie interesuje. Została zastąpiona odpowiednimi składowymi. Jeżeli ciało pozostaje na równi pochyłej to . Należy pamiętać, że gdy rozłożymy ciężar na dwie składowe to nie zajmujemy się już siłą Q, bo ona nas już nie interesuje. Została zastąpiona odpowiednimi składowymi. Jeżeli ciało pozostaje na równi pochyłej to 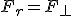 , zatem te dwie siły znoszą się wzajemnie. Pozostaje nam siła , zatem te dwie siły znoszą się wzajemnie. Pozostaje nam siła 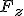 , której wartość wynosi , której wartość wynosi  jak widać z rysunku. W analogiczny sposób można obliczyć siłę jak widać z rysunku. W analogiczny sposób można obliczyć siłę 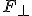 . . 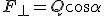 . Ten związek jest szczególnie przydatny przy analizowaniu równi pochyłej z tarciem.
1.2. Ruch ciała w dół równi pochyłej
Jeśli ciało na idealnie gładkiej równi pochyłej pozostawimy samemu sobie, to siła wypadkowa nań działająca będzie równa sile zsuwającej. Zgodnie z II zasadą dynamiki Newtona będzie się poruszać z przyspieszeniem a=Fwyp/m=mgsinα/m, zatem . Ten związek jest szczególnie przydatny przy analizowaniu równi pochyłej z tarciem.
1.2. Ruch ciała w dół równi pochyłej
Jeśli ciało na idealnie gładkiej równi pochyłej pozostawimy samemu sobie, to siła wypadkowa nań działająca będzie równa sile zsuwającej. Zgodnie z II zasadą dynamiki Newtona będzie się poruszać z przyspieszeniem a=Fwyp/m=mgsinα/m, zatem 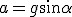 . Jeśli na ciało zadziałamy siłą F skierowaną wzdłuż równi w dół, to nasze przyspieszenie wyniesie: . Jeśli na ciało zadziałamy siłą F skierowaną wzdłuż równi w dół, to nasze przyspieszenie wyniesie: 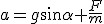 . Jeśli zaś zadziałamy siłą F, która spełnia warunek . Jeśli zaś zadziałamy siłą F, która spełnia warunek 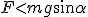 równolegle do równi, ale w jej górę, to przyspieszenie ciała wyniesie: równolegle do równi, ale w jej górę, to przyspieszenie ciała wyniesie: 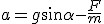 .
1.3. Ruch ciała w górę równi pochyłej
Ciało będzie się poruszało w górę równi wtedy kiedy będziemy na nie działać siłą, która powoduje ten ruch lub jeśli nadamy temu ciału odpowiednią prędkość początkową.
Załóżmy, że działamy stała siłą F równolegle do równi w jej górę. Siła F musi spełniać warunek F=mgsinα jeśli ciało ma się poruszać ruchem jednostajnym w górę równi lub F>mgsinα jeśli ciało ma się poruszać ruchem przyspieszonym w górę równi. Wtedy przyspieszenie ciała wyniesie: .
1.3. Ruch ciała w górę równi pochyłej
Ciało będzie się poruszało w górę równi wtedy kiedy będziemy na nie działać siłą, która powoduje ten ruch lub jeśli nadamy temu ciału odpowiednią prędkość początkową.
Załóżmy, że działamy stała siłą F równolegle do równi w jej górę. Siła F musi spełniać warunek F=mgsinα jeśli ciało ma się poruszać ruchem jednostajnym w górę równi lub F>mgsinα jeśli ciało ma się poruszać ruchem przyspieszonym w górę równi. Wtedy przyspieszenie ciała wyniesie: 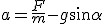
Przykład 1
Dany jest układ równi pochyłych, z których każda ma jednakową długość podstawy 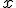 . Równie są idealnie gładkie. Dla jakiego kąta nachylenia równi do poziomu czas, po którym ciało znajdzie się u podnóża równi ma najmniejszą wartość?
Rozwiązanie:
Niech długość równi oznacza się literą . Równie są idealnie gładkie. Dla jakiego kąta nachylenia równi do poziomu czas, po którym ciało znajdzie się u podnóża równi ma najmniejszą wartość?
Rozwiązanie:
Niech długość równi oznacza się literą 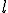 . Wiadomo, że . Wiadomo, że 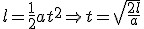 . Oczywiście jak wcześniej pisałem, na beztarciowej równi . Oczywiście jak wcześniej pisałem, na beztarciowej równi 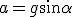 . Z kolei . Z kolei 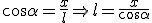 . Podstawiamy to wszystko do wzoru na czas: . Podstawiamy to wszystko do wzoru na czas: 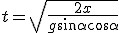 .
Iloczyn .
Iloczyn 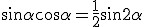 , czyli , czyli 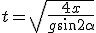 . Wartości x i g są ustalone więc czas spadku zależy tylko od kata nachylenia równi do poziomu. Ze wzoru tego widać, że czas jest minimalny wtedy kiedy funkcja sinus przyjmuje maksymalną wartość. Oczywiście wiem, że jest to 1, zatem . Wartości x i g są ustalone więc czas spadku zależy tylko od kata nachylenia równi do poziomu. Ze wzoru tego widać, że czas jest minimalny wtedy kiedy funkcja sinus przyjmuje maksymalną wartość. Oczywiście wiem, że jest to 1, zatem 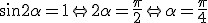 . Odp: . Odp: 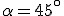
Przykład 2
Na równi pochyłej o kącie nachylenia 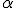 położono ciało o masie położono ciało o masie 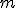 . Jakie przyspieszenia będzie miało ciało jeśli po swobodnym jego puszczeniu, działamy z zewnątrz siłą . Jakie przyspieszenia będzie miało ciało jeśli po swobodnym jego puszczeniu, działamy z zewnątrz siłą 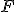 jak na rysunku? jak na rysunku?
Rozwiązanie:
Zamieściłem rysunek z rozłożona na składowe siłą F. Niech składowa równoległa do równi nazywa się 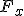 . Zgodnie z rysunkiem ma ona wartość . Zgodnie z rysunkiem ma ona wartość 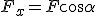 . Składowa prostopadła do równi nie będzie miała wpływu na przyspieszenia, więc nie ma co jej nawet obliczać, Przyspieszenie policzymy z II zasady dynamiki: . Składowa prostopadła do równi nie będzie miała wpływu na przyspieszenia, więc nie ma co jej nawet obliczać, Przyspieszenie policzymy z II zasady dynamiki: 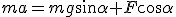 zatem zatem 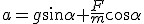
§ 2. Równia pochyła z tarciem
2.1. Rozkład sił na równi pochyłej z tarciem
Już dość dużo powiedzieliśmy na temat rozkładu siła na równi pochyłej w poprzednim punkcie. Kiedy na równi pochyłej występuje tarcie należy dodać tylko siłę tarcia: jeśli ciało porusza się w dół równi to siła tarcia jest skierowana przeciwnie do prędkości tego ciała a jeśli ciało przemieszcza się w górę równi, wówczas siła tarcia jest zwrócona tak samo jak siła zsuwająca. Siła z jaką naciska ciało na równie pochyłą jest równa 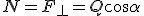 , zatem siła tarcia jest równa:
dla tarcia statycznego: , zatem siła tarcia jest równa:
dla tarcia statycznego: 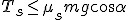 dla tarcia kinetycznego:
dla tarcia kinetycznego: 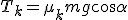 2.2. Ruch ciała w dół równi pochyłej
Jeśli ciało pozostawimy samemu sobie na nieidealnie gładkiej równi pochyłej, to ciało może, ale nie musi zacząć poruszać się w dół równi. Wszystko zależy od współczynnika tarcia statycznego ciała o powierzchnię równi pochyłej. Na ciała działają trzy siły: ciężar, siła reakcji od powierzchni równi i siła tarcia jak zwykle zwrócona przeciwnie do kierunku, w którym chce się poruszać ciało. Siła wypadkowa dwóch pierwszych siła to siła zsuwająca. Aby ciało zaczęło zsuwać się z równi pochyłej musi być spełniony warunek:
2.2. Ruch ciała w dół równi pochyłej
Jeśli ciało pozostawimy samemu sobie na nieidealnie gładkiej równi pochyłej, to ciało może, ale nie musi zacząć poruszać się w dół równi. Wszystko zależy od współczynnika tarcia statycznego ciała o powierzchnię równi pochyłej. Na ciała działają trzy siły: ciężar, siła reakcji od powierzchni równi i siła tarcia jak zwykle zwrócona przeciwnie do kierunku, w którym chce się poruszać ciało. Siła wypadkowa dwóch pierwszych siła to siła zsuwająca. Aby ciało zaczęło zsuwać się z równi pochyłej musi być spełniony warunek: 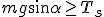 . Jak pamiętamy T=Nľs. Wcześniej wyliczona została siła nacisku: . Jak pamiętamy T=Nľs. Wcześniej wyliczona została siła nacisku: 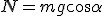 , zatem , zatem 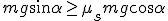 . Czyli, aby ciało zsuwało się z równi pochyłej musi zachodzić warunek: . Czyli, aby ciało zsuwało się z równi pochyłej musi zachodzić warunek:  . Jeśli . Jeśli 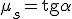 to ciało porusza sie ruchem jednostajnym prostoliniowym w dół równi. Jeśli to ciało porusza sie ruchem jednostajnym prostoliniowym w dół równi. Jeśli 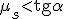 to ciało porusza się ruchem przyspieszonym w dół równi pochyłej z przyspieszeniem a, które można łatwo obliczyć. Skoro ciał porusza się w dół równi pochyłej, to nie interesuje już nas współczynnik tarcia statycznego, ale kinetycznego. Siła wypadkowa działająca na ciało wynosi to ciało porusza się ruchem przyspieszonym w dół równi pochyłej z przyspieszeniem a, które można łatwo obliczyć. Skoro ciał porusza się w dół równi pochyłej, to nie interesuje już nas współczynnik tarcia statycznego, ale kinetycznego. Siła wypadkowa działająca na ciało wynosi 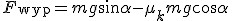 zatem zatem 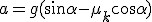 i z takim przyspieszeniem będzie poruszać się ciało w dół równi pochyłej.
2.3. Ruch ciała w górę równi pochyłej
Jeśli ciało porusza się w górę równi pochyłej, to siła tarcia działa równolegle do powierzchni równie, ale zgodnie z jej charakterystyką, przeciwnie do ruchu ciała czyli zwrócona jest w dół równi tak, że pomaga sile zsuwającej. Ciało może poruszać w górę równi pochyłej z tarciem kiedy nadamy mu odpowiednią prędkość lub działamy na nie odpowiednią siłą. Jeśli siła ta jest równoległa do powierzchni równi i działa w jej górę, to powinna spełniać warunek i z takim przyspieszeniem będzie poruszać się ciało w dół równi pochyłej.
2.3. Ruch ciała w górę równi pochyłej
Jeśli ciało porusza się w górę równi pochyłej, to siła tarcia działa równolegle do powierzchni równie, ale zgodnie z jej charakterystyką, przeciwnie do ruchu ciała czyli zwrócona jest w dół równi tak, że pomaga sile zsuwającej. Ciało może poruszać w górę równi pochyłej z tarciem kiedy nadamy mu odpowiednią prędkość lub działamy na nie odpowiednią siłą. Jeśli siła ta jest równoległa do powierzchni równi i działa w jej górę, to powinna spełniać warunek
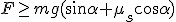 , aby ciało poruszyło się w górę równi. Jeśli , aby ciało poruszyło się w górę równi. Jeśli 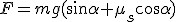 to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym a jeśli to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym a jeśli 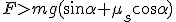 to ciało porusza się z przyspieszeniem w górę równi którego wartość wynosi: to ciało porusza się z przyspieszeniem w górę równi którego wartość wynosi: 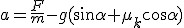
Przykład 3
Sanki ześlizgują się z pagórka, którego zbocze ma długość 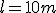 i jest nachylone pod kątem i jest nachylone pod kątem 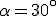 do poziomu. Jaką odległość do poziomu. Jaką odległość 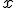 przebędą sanki na odcinku poziomym po zjechaniu ze zbocza, jeżeli na całej drodze współczynnik tarcia wynosił przebędą sanki na odcinku poziomym po zjechaniu ze zbocza, jeżeli na całej drodze współczynnik tarcia wynosił 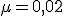 ?
Rozwiązanie:
Siła działająca na sanki na stoku jest wypadkową siły tarcia i siły zsuwającej. Po lekturze punku 2.2. wiemy, że przyspieszenie zsuwającego się ciała wynosi ?
Rozwiązanie:
Siła działająca na sanki na stoku jest wypadkową siły tarcia i siły zsuwającej. Po lekturze punku 2.2. wiemy, że przyspieszenie zsuwającego się ciała wynosi 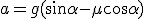 . Trzeba obliczyć prędkość sanek. Korzystamy tu w wyprowadzonej w temacie: Ruchy prostoliniowe zależności dla ruchu przyspieszonego: . Trzeba obliczyć prędkość sanek. Korzystamy tu w wyprowadzonej w temacie: Ruchy prostoliniowe zależności dla ruchu przyspieszonego: 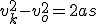 . U nas . U nas 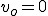 oraz oraz 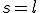 . Zatem . Zatem 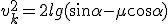 . I już jesteśmy na płaskim. Teraz jedyną siłą działającą na ciało jest siła tarcia skierowana przeciwnie do kierunku ruchu ciała, zatem będzie to ruch przyspieszony. Skoro jesteśmy na płaskim podłożu, to siła tarcia wyniesie . I już jesteśmy na płaskim. Teraz jedyną siłą działającą na ciało jest siła tarcia skierowana przeciwnie do kierunku ruchu ciała, zatem będzie to ruch przyspieszony. Skoro jesteśmy na płaskim podłożu, to siła tarcia wyniesie 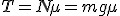 a więc przyspieszenie ciała na płaskim podłożu wyniesie a więc przyspieszenie ciała na płaskim podłożu wyniesie 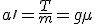 . Dalej rozpatrujemy ruch opóźniony. Tym razem skorzystamy z zależności analogicznej jak poprzednio, ale dla ruchu opóźnionego: . Dalej rozpatrujemy ruch opóźniony. Tym razem skorzystamy z zależności analogicznej jak poprzednio, ale dla ruchu opóźnionego:  . U nas pamiętamy, że nasza prędkość u podstawy równi będzie jednocześnie prędkością początkową ruchu opóźnionego . U nas pamiętamy, że nasza prędkość u podstawy równi będzie jednocześnie prędkością początkową ruchu opóźnionego 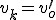 . Kiedy ciało się zatrzyma to . Kiedy ciało się zatrzyma to 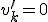 i i  , zatem , zatem 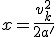
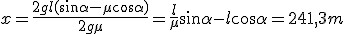
Przykład 4
Na równi pochyłej o kącie nachylenia 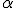 znajdują się dwa, z których jedno jest zaopatrzone w dynamometr (rysunek). Obliczyć jaką siłę znajdują się dwa, z których jedno jest zaopatrzone w dynamometr (rysunek). Obliczyć jaką siłę  wskaże dynamometr jeśli ciało o masie wskaże dynamometr jeśli ciało o masie 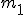 porusza się z tarciem (współczynnik tarcia wynosi porusza się z tarciem (współczynnik tarcia wynosi 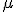 ), a ciało o masie ), a ciało o masie 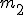 porusza się bez tarcia. porusza się bez tarcia.
Rozwiązanie:
Na powyższym rysunku zaznaczyłem siły jakie działają na poszczególne masy. Przypomnę, że dynamometr wskazuje takie siły, jakie na niego działają. Założyłem, że dynamometr jest nieważki i połączony z ciałem o masie 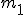 .
Ciało o masie .
Ciało o masie 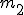 działa na ciało dynamometr siłą działa na ciało dynamometr siłą 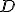 , więc dynamometr działa na to ciało siła , więc dynamometr działa na to ciało siła 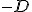 . Skoro dynamometr i ciało masie . Skoro dynamometr i ciało masie 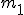 można traktować jako jedno ciało, to na to ciało działa siła można traktować jako jedno ciało, to na to ciało działa siła 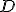 . O pozostałych siłach (tarcie i siła zsuwająca) chyba nie muszę już mówić. Poza tym należy zauważyć, że ciała będą miały jednakowe przyspieszenia, bo kiedy się połączą to o przyspieszaniu ciała . O pozostałych siłach (tarcie i siła zsuwająca) chyba nie muszę już mówić. Poza tym należy zauważyć, że ciała będą miały jednakowe przyspieszenia, bo kiedy się połączą to o przyspieszaniu ciała 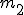 będzie decydował ruch o masie będzie decydował ruch o masie 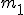 . Czas na równania Newtona: . Czas na równania Newtona:
Najlepiej wyznaczyć przyspieszenie z jednego równania i wstawić do następnego, gdyż przyspieszenie nas nie interesuje:
|
 |
|
|