 |
 |
 |
    |
|
Ruchy krzywoliniowe
Ruchy krzywoliniowe
Jak sama nazwa wskazuje, ruch krzywoliniowy dotyczy sytuacji kiedy ciało nie porusza się po linii prostej a jego ruch opisują przynajmniej dwie współrzędne. Takie właśnie ruchy będziemy tutaj opisywać.
.
§ 1. Przyspieszenie: składowa styczna i normalna
1.1. Postać matematyczna
Odwołując się do geometrii różniczkowej (I wzór Freneta) można wykazać, że przyspieszenie ciała w ruchu krzywoliniowym wyraża się wzorem:
Składowa styczna i normalna przyspieszenia
gdzie
 - przyspieszenie styczne, - przyspieszenie styczne,
 - jednostkowy wektor styczny do toru, - jednostkowy wektor styczny do toru,
 - przyspieszenie normalne, - przyspieszenie normalne,
 - krzywizna krzywej po jakiej porusza się ciało, - krzywizna krzywej po jakiej porusza się ciało,
 - wektor jednostkowy zwrócony do środka krzywizny krzywej.
1.2. Wartość przyspieszenia w ruchu krzywoliniowym
Wartość przyspieszenia w ruchu krzywoliniowym wynosi - wektor jednostkowy zwrócony do środka krzywizny krzywej.
1.2. Wartość przyspieszenia w ruchu krzywoliniowym
Wartość przyspieszenia w ruchu krzywoliniowym wynosi

Nietrudno zauważyć, że gdy mamy do czynienia z ruchem prostoliniowym krzywizna krzywej jest nieskończona, więc nie ma sensu rozpatrywać składowej normalnej przyspieszenia, która znika.
W ruchu jednostajnym prostoliniowym pomijamy także przyspieszenie styczne.
W ruchu jednostajnie przyspieszonym (opóźnionym) prostoliniowym uwzględniamy tylko przyspieszenie styczne.
W ruchu krzywoliniowym prędkość nie zawsze tworzy kąt zerowy z wektorem przyspieszenia. Jeśli kąt pomiędzy tymi wektorami oznaczymy jako  , to zachodzą następujące zależności: , to zachodzą następujące zależności:
 - mamy ruch przyspieszony, - mamy ruch przyspieszony,
 - mamy ruch jednostajny po okręgu (niekoniecznie po okręgu, ale tutaj takim ruchem będziemy się zajmować), - mamy ruch jednostajny po okręgu (niekoniecznie po okręgu, ale tutaj takim ruchem będziemy się zajmować),
 - mamy ruch opóźniony.
1.3. Interpretacja fizyczna składowej stycznej i normalnej przyspieszenia
Warto zapamiętać z czym wiążą się oba rodzaje przyspieszeń: - mamy ruch opóźniony.
1.3. Interpretacja fizyczna składowej stycznej i normalnej przyspieszenia
Warto zapamiętać z czym wiążą się oba rodzaje przyspieszeń:
- przyspieszenie styczne jest odpowiedzialne za zmianę wartości prędkości
- przyspieszenie normalne (dośrodkowe) odpowiada za zmianę kierunku wektora prędkości
§ 2. Ruch jednostajny po okręgu
2.1. Definicja
Jest to ruch, w którym torem, po jakim porusza się ciało, jest okrąg a wartość prędkości nie ulega zmianie.
Krzywizną krzywej w ruchu po okręgu jest oczywiście promień okręgu  .
2.2. Siła dośrodkowa
Z pojęciem siły można zapoznać się w temacie Zasady dynamiki Newtona.
2.2.1. Istota siły dośrodkowej
Z definicji siły wynika, że siła dośrodkowa nie jest żadną nową siłą, lecz jest to każda siła, która powoduje ruch po okręgu. Zatem rzec można, że siła dośrodkowa jest rolą jaką przyjmą inne siły powodujące ruch ciała po okręgu. Np. siła grawitacji w ruchu satelity wokół Ziemi pełni rolę siły dośrodkowej; siła elektrostatyczna pełni rolę siły dośrodkowej w ruchu elektronu po jednej z orbit. Podobnie jest z siłą Lorentza.
2.2.2. Cechy siły dośrodkowej .
2.2. Siła dośrodkowa
Z pojęciem siły można zapoznać się w temacie Zasady dynamiki Newtona.
2.2.1. Istota siły dośrodkowej
Z definicji siły wynika, że siła dośrodkowa nie jest żadną nową siłą, lecz jest to każda siła, która powoduje ruch po okręgu. Zatem rzec można, że siła dośrodkowa jest rolą jaką przyjmą inne siły powodujące ruch ciała po okręgu. Np. siła grawitacji w ruchu satelity wokół Ziemi pełni rolę siły dośrodkowej; siła elektrostatyczna pełni rolę siły dośrodkowej w ruchu elektronu po jednej z orbit. Podobnie jest z siłą Lorentza.
2.2.2. Cechy siły dośrodkowej
- nie jest żadna nową siłą, gdyż nie wynika z oddziaływań między ciałami,
- jej wartość wynosi
 , ,
- inne siły rzeczywiste pełnią jej rolę (nazwa siła dośrodkowa jest przypisana siłom, które powodują ruch po okręgu),
- jest skierowana do środka okręgu wzdłuż jego promienia
 . .
2.3. Wielkości kinematyczne opisujące ruch jednostajny po okręgu
2.3.1. Układ współrzędnych biegunowych
Ruchy w jednym wymiarze (czasami także we dwóch) opisuje się w tzw. kartezjańskim (prostokątnym) układzie współrzędnych a współrzędne opisujące ten ruch nazywa się współrzędnymi kartezjańskimi lub prostokątnymi  .
Z ruchem po okręgu jest inaczej. Opisuje się go na płaszczyźnie w tzw. układzie współrzędnych biegunowych .
Z ruchem po okręgu jest inaczej. Opisuje się go na płaszczyźnie w tzw. układzie współrzędnych biegunowych  . Współrzędna . Współrzędna  to odległość ciała od początku układu współrzędnych a to odległość ciała od początku układu współrzędnych a  to położenie kątowe ciała, czyli kąt jaki tworzy wektor wodzący punktu z osią x. Ruch po okręgu łatwiej opisuje się w układzie współrzędnych biegunowych, gdyż jeśliby opisywać taki ruch w układzie prostokątnym to trzeba by było uwzględniać ciągłe zmiany współrzędnych to położenie kątowe ciała, czyli kąt jaki tworzy wektor wodzący punktu z osią x. Ruch po okręgu łatwiej opisuje się w układzie współrzędnych biegunowych, gdyż jeśliby opisywać taki ruch w układzie prostokątnym to trzeba by było uwzględniać ciągłe zmiany współrzędnych 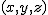 , a tak, w układzie , a tak, w układzie  , notujemy zmianę tylko jednej współrzędnej - , notujemy zmianę tylko jednej współrzędnej -  , gdyż , gdyż  jest stałe (promień okręgu).
2.3.2. Wielkości kinematyczne w ruchu po okręgu
2.3.2.1. Położenie kątowe
Położenie kątowe jest to stosunek długości łuku do promienia okręgu. jest stałe (promień okręgu).
2.3.2. Wielkości kinematyczne w ruchu po okręgu
2.3.2.1. Położenie kątowe
Położenie kątowe jest to stosunek długości łuku do promienia okręgu.

gdzie
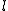 - długość łuku, - długość łuku,
 - promień okręgu.
2.3.2.2. Droga kątowa
Droga kątowa jest długością łuku jaki pokonało ciało w danym czasie. - promień okręgu.
2.3.2.2. Droga kątowa
Droga kątowa jest długością łuku jaki pokonało ciało w danym czasie.
gdzie
 - długość łuku.
2.3.2.3. Szybkość kątowa
Szybkość kątowa jest pochodną położenia kątowego po czasie lub szybkość kątowa jest zmianą położenia kątowego w czasie.
Definicje szkolne - długość łuku.
2.3.2.3. Szybkość kątowa
Szybkość kątowa jest pochodną położenia kątowego po czasie lub szybkość kątowa jest zmianą położenia kątowego w czasie.
Definicje szkolne
 lub lub 
Definicja akademicka
2.3.2.4. Okres
Okresem nazywamy czas, po którym ciało powraca do miejsca, w którym się pierwotnie znajdowało.
Okres oznacza się dużą literą  i nazywa nieraz czasem cyklu.
2.3.2.5. Częstotliwość
Częstotliwość jest to odwrotność okresu lub ilość cykli pokonanych w danej jednostce czasu. i nazywa nieraz czasem cyklu.
2.3.2.5. Częstotliwość
Częstotliwość jest to odwrotność okresu lub ilość cykli pokonanych w danej jednostce czasu.
Częstotliwość oznacza się także grecką literą  . Oznaczenie . Oznaczenie  pochodzi z języka angielskiego, frequency - częstotliwość.
2.3.3. Związek między prędkością liniową i kątową
Jeśli czas jednego pełnego okrążenia oznaczymy jako T to szybkość ciała jest stała i równa pochodzi z języka angielskiego, frequency - częstotliwość.
2.3.3. Związek między prędkością liniową i kątową
Jeśli czas jednego pełnego okrążenia oznaczymy jako T to szybkość ciała jest stała i równa  co wiąże prędkość ruchu postępowego z prędkością kątową.
Jednakże ścisły związek pomiędzy tymi wielkościami wyraża się zależnością co wiąże prędkość ruchu postępowego z prędkością kątową.
Jednakże ścisły związek pomiędzy tymi wielkościami wyraża się zależnością
Kierunek wektora prędkości kątowej jest prostopadły do płaszczyzny w jakiej opisujemy ruch.
2.3. Równanie ruchu jednostajnego po okręgu
Okazuje się, że równanie ruchu ciała poruszającego się po okręgu wygląda we współrzędnych biegunowych identycznie jak równanie ruchu jednostajnego we współrzędnych kartezjańskich.
Przykład 1
Jest godzina 12. Po jakim czasie wskazówka godzinowa i minutowa ponownie pokryją się?
Rozwiązanie:
Niech T - okres obiegu wskazówki minutowej (T=60 min). Czas po jakim wskazówki minutowa i godzinowa znowu się pokryją (licząc od ustawienia początkowego) będzie równy τ=T+t, gdzie T - czas po jakim wskazówka minutowa obiegnie tarczę zegara, t - czas liczony od ustawienia po czasie T. Po czasie T:
wskazówka minutowa:  .
wskazówka godzinowa .
wskazówka godzinowa  . Aby wskazówki się pokryły położenia kątowe wskazówki godzinowej i minutowej muszą być takie same: . Aby wskazówki się pokryły położenia kątowe wskazówki godzinowej i minutowej muszą być takie same:  .
Odpowiedź: .
Odpowiedź:
Przykład 2
W wierzchołka góry wyrzucono ciało w kierunku poziomym z prędkością  . Znaleźć składowe wektora przyspieszenia, styczną i normalną do toru, po czasie . Znaleźć składowe wektora przyspieszenia, styczną i normalną do toru, po czasie  od chwili wyrzucenia. od chwili wyrzucenia.  .
Rozwiązanie:
Rozkładając prędkość na składowe .
Rozwiązanie:
Rozkładając prędkość na składowe  i i  oraz przyspieszenie g na składową normalną oraz przyspieszenie g na składową normalną  i styczną i styczną  zauważamy, że zauważamy, że  . Ponadto wiemy, że . Ponadto wiemy, że  oraz oraz  , zatem , zatem  .
Składowa normalna będzie liczona ze wzoru .
Składowa normalna będzie liczona ze wzoru
 . Odpowiedź: . Odpowiedź:  . .
§ 3. Ruch jednostajnie przyspieszony po okręgu
3.1. Definicja
Jest to ruch, w którym torem po jakim porusza się ciało jest okrąg i wartość prędkości kątowej w jednakowych odstępach czasu wzrasta o tę samą wartość.
W ruchu tym wektor przyspieszenia kątowego ma ten sam zwrot co wektor prędkości kątowej.
3.2. Przyspieszenie kątowe
Przyspieszeniem kątowym nazywa się zmianę szybkości kątowej w czasie.
Definicja szkolna
Definicja akademicka
3.3. Związek między przyspieszeniem kątowym i liniowym
Łatwo można otrzymać związek pomiędzy przyspieszeniem kątowym a liniowym. Wiemy, że  , zatem , zatem  . Jednakże ścisły związek pomiędzy tymi wielkościami wyraża się zależnością . Jednakże ścisły związek pomiędzy tymi wielkościami wyraża się zależnością
Kierunek wektora przyspieszenia kątowego jest prostopadły do płaszczyzny w jakiej opisujemy ruch.
3.4. Równania ruchu jednostajnie przyspieszonego po okręgu
Równania ruchu jednostajnie przyspieszonego po okręgu są analogiczne jak dla ruchu jednostajnie przyspieszonego po linii prostej z tą jednak różnicą, że w ruchu po okręgu używamy współrzędnych biegunowych.
Równania ruchu jednostajnie przyspieszonego po okręgu
§ 4. Ruch jednostajnie opóźniony po okręgu
4.1. Definicja
Jest to ruch, w którym torem po jakim porusza się ciało jest okrąg i wartość prędkości kątowej w jednakowych odstępach czasu maleje o tę samą wartość
4.2. Równania ruchu jednostajnie opóźnionego po okręgu
Równania ruchu jednostajnie opóźnionego po okręgu są analogiczne jak dla ruchu jednostajnie opóźnionego po linii prostej z tą jednak różnicą, że w ruchu po okręgu używamy współrzędnych biegunowych.
Równania ruchu jednostajnie opóźnionego po okręgu
|
 |
|
|