 |
 |
 |
    |
|
Ruchy prostoliniowe
Ruchy prostoliniowe
W tym temacie zajmował się będę ruchem posuwistym (translacyjnym), czyli ruchem, w którym ciało nie wykonuje obrotów. Do opisu takiego ruchu, przydatną idealizacją jest punkt materialny. Jest to ciało obdarzone masą, o rozmiarach geometrycznych znikomych (zerowa objętość), bądź znikomych w porównaniu z odległościami jakie przebywa. Na przykład, elektron poruszający się w lampie elektronowej jest punktem materialnym. Podobnie Ziemia w ruchu wokół Słońca może być bez obaw traktowana jako punkt materialny. Jednakże przy obliczaniu zmian przyspieszenia ziemskiego wraz z szerokością geograficzną, Ziemi nie można traktować jako punktu materialnego. W końcu, ruch samochodu, sanek, pociągu, loty ptaków traktować będę jako ruchu PM.
Opis każdego ruchu zależy od konkretnego obserwatora, dlatego ciało względem którego analizujemy przemieszczanie się danego obiektu nazywamy układem odniesienia. Cechę tę nazywamy względnością ruchu. Jest to jedna z wersji podstawowej zasady fizyki - zasady względności Galileusza, która stanowi punkt wyjścia dla szczególnej teorii względności Alberta Einsteina.
W poniższych rozważaniach, korzystał będę z podstaw rachunku wektorowego. Dla dobrego zrozumienia tematu, potrzebne jest zrozumienie jego istoty i reprezentacji geometrycznej..
§ 0. Podstawowe definicje
Układ odniesienia jest to obiekt fizyczny względem którego obserwowane jest dane zjawisko fizyczne.
Położenie  jest to wektor mający początek w początku wybranego układu odniesienia a koniec w punkcie, w którym znajduje się ciało. Jest to wektor wodzący ciała. Oznaczenie pochodzi z języka angielskiego, radius vector - wektor wodzący.
Tor jest to linia/krzywa po jakiej porusza się ciało.
Droga jest to wektor mający początek w początku wybranego układu odniesienia a koniec w punkcie, w którym znajduje się ciało. Jest to wektor wodzący ciała. Oznaczenie pochodzi z języka angielskiego, radius vector - wektor wodzący.
Tor jest to linia/krzywa po jakiej porusza się ciało.
Droga 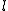 lub lub  jest to długość kawałka toru po jakim porusza się ciało; Drogą może zatem być długość odcinka (ruch prostoliniowy) lub długość łuku krzywej (ruch krzywoliniowy). Jednostką drogi w układzie SI jest metr: jest to długość kawałka toru po jakim porusza się ciało; Drogą może zatem być długość odcinka (ruch prostoliniowy) lub długość łuku krzywej (ruch krzywoliniowy). Jednostką drogi w układzie SI jest metr:  .
Prędkość .
Prędkość  jest to zmiana położenia w czasie. Oznaczenie pochodzi z języka angielskiego, velocity - prędkość.
Definicja szkolna jest to zmiana położenia w czasie. Oznaczenie pochodzi z języka angielskiego, velocity - prędkość.
Definicja szkolna
Definicja akademicka
Wektor prędkości jest zawsze styczny do toru.
Szybkość jest wartością prędkości.
Jednostką szybkości jest metr na sekundę:  .
Przyspieszenie .
Przyspieszenie  jest to zmiana prędkości w czasie. Oznaczenie pochodzi z języka angielskiego, acceleration - przyspieszenie.
Definicja szkolna jest to zmiana prędkości w czasie. Oznaczenie pochodzi z języka angielskiego, acceleration - przyspieszenie.
Definicja szkolna
Definicja akademicka
Jednostką przyspieszenia w układzie SI jest metr na sekundę kwadrat:  .
Na początku dobrze jest zapoznać się z następującymi oznaczeniami: .
Na początku dobrze jest zapoznać się z następującymi oznaczeniami:
 - współrzędna położenia ciała w chwili - współrzędna położenia ciała w chwili  , ,
 - współrzędna położenia ciała w chwili - współrzędna położenia ciała w chwili  , ,
 - prędkość jaką posiada ciało w chwili - prędkość jaką posiada ciało w chwili 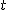 , ,
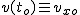 - prędkość jaką posiada ciało w chwili - prędkość jaką posiada ciało w chwili  , ,
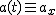 - przyspieszenie ciała w chwili - przyspieszenie ciała w chwili  . .
§ 1. Ruch jednostajny prostoliniowy
1.1. Definicja
Jest to ruch, w którym ciało w jednakowych odstępach czasu przebywa jednakowe odcinki drogi.
Z definicji tej wynikają następujące wnioski:
- droga jest wprost proporcjonalna do czasu
- każdy rodzaj przyspieszenia (styczne, normalne, rotacyjne itd.) jest równy zeru
- ciało ma przez cały czas trwania ruchu stałą prędkość
1.2. Równanie ruchu jednostajnego prostoliniowego
Powołując się na zasady dynamiki Newtona można pokazać, że jeśli wypadkowa siła działająca na ciało jest równa zeru to jednowymiarowe równanie ruchu jednostajnego prostoliniowego wygląda następująco
Oczywiście wygodnie jest się posługiwać notacją  , zatem równanie ruchu jednostajnego będzie miało postać , zatem równanie ruchu jednostajnego będzie miało postać
1.3. Przykładowe wykresy
Przykład 1
Rowerzysta wyjeżdża z miejscowości i A i porusza się ze stałą szybkością  . Pół godziny po nim . Pół godziny po nim  również z miejscowości A wyrusza kierowca samochodem i porusza się ze stałą szybkością również z miejscowości A wyrusza kierowca samochodem i porusza się ze stałą szybkością  . W jakiej odległości od miejscowości A i po jakim czasie kierowca dogodni rowerzystę?
Rozwiązanie:
Kierowca i rowerzysta spotkają się wtedy, kiedy drogi przez nich pokonane będą równe.
Rozpatrzmy sytuację po upływie czasu . W jakiej odległości od miejscowości A i po jakim czasie kierowca dogodni rowerzystę?
Rozwiązanie:
Kierowca i rowerzysta spotkają się wtedy, kiedy drogi przez nich pokonane będą równe.
Rozpatrzmy sytuację po upływie czasu  . Rowerzysta przebył drogę równą . Rowerzysta przebył drogę równą  a kierowca dopiero rozpoczął swój ruch, więc jego położenie początkowe jest równe zeru. R-nie ruchu rowerzysty: a kierowca dopiero rozpoczął swój ruch, więc jego położenie początkowe jest równe zeru. R-nie ruchu rowerzysty:  . R-nie ruchu kierowcy: . R-nie ruchu kierowcy:  . Przyrównujemy oba równania i mamy . Przyrównujemy oba równania i mamy  . Zadanie można też rozwiązać wykorzystując pojęcie szybkości względnej. Problem ten pozostawiam potencjalnemu Czytelnikowi. . Zadanie można też rozwiązać wykorzystując pojęcie szybkości względnej. Problem ten pozostawiam potencjalnemu Czytelnikowi.
§ 2. Ruch jednostajnie przyspieszony prostoliniowy
2.1. Definicja
Jest to ruch, w którym w jednakowych odstępach czasu wartość prędkości (szybkość) wzrasta o tę samą wartość.
Z definicji tej wynikają następujące wnioski:
- przyspieszenie styczne ciała jest różne i większe od zera, pozostałe rodzaje przyspieszenia są równe zeru
- przyspieszenie ciała jest stałe
- kolejne odcinki drogi mają się do siebie jak kolejne liczby nieparzyste
- wektor przyspieszenia i prędkości mają ten sam kierunek i zwrot
2.2. Równania ruchu jednostajnie przyspieszonego prostoliniowego
Powołując się na zasady dynamiki Newtona można pokazać, że jeśli wypadkowa siła działająca na ciało jest stała i różna od zera, to jednowymiarowe[1] równania ruchu jednostajnie przyspieszonego prostoliniowego można zapisać w jednej z poniższych postaci. Przyjmuję tutaj 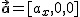 , ,  , ,  .
Równania ruchu jednostajnie przyspieszonego prostoliniowego .
Równania ruchu jednostajnie przyspieszonego prostoliniowego
Wygodnie jest się posługiwać notacją  , ,  , zatem np. pierwsze dwa równania można zapisać jako , zatem np. pierwsze dwa równania można zapisać jako
2.3. Przykładowe wykresy
Przykład 2
Ciało w ciągu  -tej sekundy ruchu przebyło drogę -tej sekundy ruchu przebyło drogę  . Jakie jest przyspieszenie tego ciała? O ile wzrosła szybkość tego ciała w przeciągu . Jakie jest przyspieszenie tego ciała? O ile wzrosła szybkość tego ciała w przeciągu  -tej sekundy?
Rozwiązanie:
Rozpatrzmy przedziały czasowe
0-1 → 1 sekunda
1-2 → 2 sekunda
2-3 → 3 sekunda
3-4 → 4 sekunda
... -tej sekundy?
Rozwiązanie:
Rozpatrzmy przedziały czasowe
0-1 → 1 sekunda
1-2 → 2 sekunda
2-3 → 3 sekunda
3-4 → 4 sekunda
...
 → →  -ta sekunda
Czyli droga jaką ciało przebyło w -ta sekunda
Czyli droga jaką ciało przebyło w  -tej sekundzie to inaczej droga jaką przebyło ciało do -tej sekundzie to inaczej droga jaką przebyło ciało do  -tej sekundy minus droga przebyta przez to ciało do -tej sekundy minus droga przebyta przez to ciało do 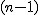 -tej sekundy. -tej sekundy. 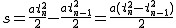 . Co daje . Co daje  . Zmiana szybkości to inaczej . Zmiana szybkości to inaczej  , a zatem podstawiając za przyspieszenie przedostatnie równanie otrzymujmy , a zatem podstawiając za przyspieszenie przedostatnie równanie otrzymujmy . .
§ 3. Ruch jednostajnie opóźniony prostoliniowy
3.1. Definicja
Jest to ruch, w którym w jednakowych odstępach czasu wartość prędkości (szybkość) maleje o tę samą wartość.
Z definicji tej wynikają następujące wnioski:
- przyspieszenie styczne ciała jest różne i mniejsze od zera, pozostałe rodzaje przyspieszenia są równe zeru
- przyspieszenie ciała jest stałe
- wektor przyspieszenia i prędkości mają przeciwnie kierunek i zwrot
3.2. Równania ruchu jednostajnie opóźnionego prostoliniowego
Powołując się na zasady dynamiki Newtona można pokazać, że jeśli wypadkowa siła działająca na ciało jest stała i różna od zera to równanie ruchu jednostajnie przyspieszonego prostoliniowego można zapisać w jednej z poniższych postaci. Przyjmuję tutaj 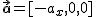 , ,  , ,  .
Równania ruchu jednostajnie opóźnionego prostoliniowego .
Równania ruchu jednostajnie opóźnionego prostoliniowego
Wygodnie jest się posługiwać notacją  , , 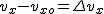 , zatem np. pierwsze dwa równania można zapisać jako , zatem np. pierwsze dwa równania można zapisać jako
3.3. Przykładowe wykresy
Przykład 3
Samochód testowy został rozpędzony do szybkości  . Po uzyskaniu tej szybkości w samochodzie włączył się mechanizm hamujący. W przeciągu czasu . Po uzyskaniu tej szybkości w samochodzie włączył się mechanizm hamujący. W przeciągu czasu  przebył drogę przebył drogę  . Czy samochód zdąży zatrzymać się przed stertą opon oddaloną od niego o . Czy samochód zdąży zatrzymać się przed stertą opon oddaloną od niego o  ?
Rozwiązanie:
Stosujemy wzór ?
Rozwiązanie:
Stosujemy wzór  . Samochód się zatrzymuje, więc . Samochód się zatrzymuje, więc  . Przyspieszenie można policzyć z przekształconego wzoru na drogę: . Przyspieszenie można policzyć z przekształconego wzoru na drogę:  , zatem , zatem  . .
Dodatek - prędkość względna, ujęcie klasyczne
Jeśli dwa ciała (1 i 2) poruszają się z jakąś prędkością, to różną prędkość ciała (1) zanotuje obserwator stojący nieruchomo (O) a inną obserwator (2) poruszający się.
Prędkość względna to prędkość jednego ciała w układzie drugiego ciała. Odpowiada to sytuacji gdyby jeden obserwator się zatrzymał a drugi zyskał lub stracił prędkość, tą która posiadał obserwator, który się zatrzymał. Można rozpatrzyć trzy przypadki jednowymiarowe:
Ciało  ma prędkość ma prędkość  a ciało a ciało  prędkość prędkość  (a) ciała poruszają się w te samą stronę
(a) ciała poruszają się w te samą stronę
(b) ciała poruszają się w przeciwne strony
(c) ciało  porusza się z prędkością porusza się z prędkością  a ciało a ciało  stoi nieruchomo
W układzie ciała stoi nieruchomo
W układzie ciała  to obserwator to obserwator 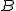 się porusza się z się porusza się z  a a 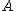 stoi; za to w układzie ciała stoi; za to w układzie ciała  to ciało to ciało 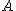 ma prędkość ma prędkość 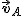 a ciało a ciało 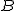 jest nieruchome. jest nieruchome.
[1] Przez ruch jednowymiarowy rozumiem tutaj ruch wzdłuż osi x prostokątnego układu współrzędnych xyz. Dodatkowo zawsze tam gdzie zaznaczę, że ruch jest jednowymiarowy bądź odbywa się wzdłuż prostej, co jest równoważne ruchowi w jednym wymiarze, przyjmuję  , ,  . .
|
 |
|
|