 |
 |
 |
    |
|
Rzuty w polu grawitacyjnym
Rzuty w polu grawitacyjnym
Z pojęciem rzutu w polu grawitacyjnym Czytelnik na pewno się już spotkał w gimnazjum. Tutaj nieco uzupełnimy tę wiedzę. Skupimy się głównie na opisie matematycznym tych ruchów. W poniższym temacie zakładamy, że pole grawitacyjne, w którym ma miejsce rzut jest jednorodne, tzn. 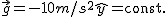 . Dodatkowo pomijamy wszelkie opory ruchu. Okazuje się, że każdy ruch w takim polu sił można opisać już za pomocą dwóch współrzędnych, tzn. ruch sprowadza się do ruchu w płaszczyźnie. W niniejszym opracowaniu będę stosował układ współrzędnych Oxy. Przed przestudiowaniem tego opracowania radziłbym zapoznać się z tematem Ruchy prostoliniowe. . Dodatkowo pomijamy wszelkie opory ruchu. Okazuje się, że każdy ruch w takim polu sił można opisać już za pomocą dwóch współrzędnych, tzn. ruch sprowadza się do ruchu w płaszczyźnie. W niniejszym opracowaniu będę stosował układ współrzędnych Oxy. Przed przestudiowaniem tego opracowania radziłbym zapoznać się z tematem Ruchy prostoliniowe.
§ 0. Oznaczenia, typy rzutów i podstawowe definicje
Do wszystkich poniższych rozważań proponuję przyjąć następujące oznaczenia:
 - wysokość na jakiej znajduje się ciało w danej chwili czasu, - wysokość na jakiej znajduje się ciało w danej chwili czasu,
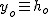 - wysokość na jakiej znajduje się ciało w czasie - wysokość na jakiej znajduje się ciało w czasie 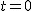 , ,
 - prędkość ciała w danej chwili czasu, - prędkość ciała w danej chwili czasu,
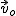 - prędkość początkowa (prędkość jaką nadajemy ciału), - prędkość początkowa (prędkość jaką nadajemy ciału),
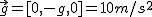 - przyspieszenie ziemskie (oś Oy kierujemy tak aby przyspieszenie ziemskie miało tylko jedną składową - pionową. Ponadto Oś Oy jest zwrócona grotem do góry).
W tym opracowaniu będziemy zajmowali się kilkoma rodzajami rzutów w polu grawitacyjnym. Poniżej przedstawię ich skrócone charakterystyki.
Spadek swobodny - prędkość początkowa jest równa zeru, wysokość początkowa różna od zera, ruch odbywa się wzdłuż linii prostej.
Rzut pionowy w górę - prędkość początkowa różna od zera i zwrócona przeciwnie do g, wysokość początkowa różna od zera lub równa zeru, ruch odbywa się wzdłuż linii prostej.
Rzut pionowy w dół - prędkość początkowa różna od zera i zwrócona zgodnie z g, wysokość początkowa różna od zera, ruch odbywa się wzdłuż linii prostej.
Rzut poziomy - prędkość początkowa różna od zera, skierowana prostopadle do g, wysokość początkowa różna od zera, ruch odbywa się w płaszczyźnie.
Rzut ukośny - prędkość początkowa różna od zera, skierowana pod kątem różnym od zera do poziomu, wysokość równa zeru; (można rozpatrzyć z niezerową wysokością początkową, ale jest to dość skomplikowane) - przyspieszenie ziemskie (oś Oy kierujemy tak aby przyspieszenie ziemskie miało tylko jedną składową - pionową. Ponadto Oś Oy jest zwrócona grotem do góry).
W tym opracowaniu będziemy zajmowali się kilkoma rodzajami rzutów w polu grawitacyjnym. Poniżej przedstawię ich skrócone charakterystyki.
Spadek swobodny - prędkość początkowa jest równa zeru, wysokość początkowa różna od zera, ruch odbywa się wzdłuż linii prostej.
Rzut pionowy w górę - prędkość początkowa różna od zera i zwrócona przeciwnie do g, wysokość początkowa różna od zera lub równa zeru, ruch odbywa się wzdłuż linii prostej.
Rzut pionowy w dół - prędkość początkowa różna od zera i zwrócona zgodnie z g, wysokość początkowa różna od zera, ruch odbywa się wzdłuż linii prostej.
Rzut poziomy - prędkość początkowa różna od zera, skierowana prostopadle do g, wysokość początkowa różna od zera, ruch odbywa się w płaszczyźnie.
Rzut ukośny - prędkość początkowa różna od zera, skierowana pod kątem różnym od zera do poziomu, wysokość równa zeru; (można rozpatrzyć z niezerową wysokością początkową, ale jest to dość skomplikowane)
§ 1. Spadek swobodny
Jest to ruch bez prędkości początkowej, zatem mamy swoisty spadek, w potocznym tego słowa znaczeniu. Na ciało działa tylko jedna siła - siła grawitacji, która powoduje przyspieszenie ciała w kierunku pionowym w dół. Zgodnie z II zasadą dynamiki, takie ciało porusza się ruchem jednostajnie przyspieszonym.
1.1. Równanie ruchu
Równanie spadku swobodnego jest analogiczne do ruchu jednostajnie przyspieszonego bez prędkości początkowej (patrz linkowany temat)
znak "-" bo oś Oy jest skierowana do góry (patrz oznaczenia).
1.2. Czas spadku
Rozpatrzmy czas spadku z wysokości 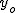 na dowolną wysokość na dowolną wysokość 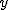 . Wiadomo, że "delta to od końca odjąć początek", zatem . Wiadomo, że "delta to od końca odjąć początek", zatem 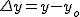 . Oczywistym jest, że wysokość końcowa jest mniejsza od wysokości początkowej więc . Oczywistym jest, że wysokość końcowa jest mniejsza od wysokości początkowej więc 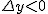 ; niemniej jednak nas nie interesuje znak wyrażenia ; niemniej jednak nas nie interesuje znak wyrażenia 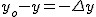 , zatem , zatem
Rozwiązując to równanie względem 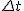 otrzymujemy wynik
Czas spadku na dowolną wysokość w spadku swobodnym otrzymujemy wynik
Czas spadku na dowolną wysokość w spadku swobodnym
W szczególności, gdy ciało spada na poziom 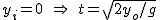
Przykład 1
Ciało spada swobodnie z wysokości 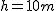 . Z jaką prędkością ciało uderzy o ziemię? Na jakiej wysokości . Z jaką prędkością ciało uderzy o ziemię? Na jakiej wysokości  prędkość ciała będzie równa połowie prędkości końcowej? Przyjmij prędkość ciała będzie równa połowie prędkości końcowej? Przyjmij 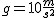 Rozwiązanie:
Najpierw policzymy czas spadku na poziom zerowy,
Rozwiązanie:
Najpierw policzymy czas spadku na poziom zerowy, 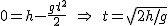 . Korzystając z tego, że w spadku swobodnym . Korzystając z tego, że w spadku swobodnym 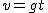 mamy mamy 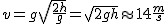 . Niech . Niech 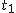 będzie momentem, kiedy ciało znajduje się na wysokości będzie momentem, kiedy ciało znajduje się na wysokości 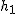 i ma prędkość i ma prędkość 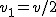 .
Równanie spadku swobodnego wygląda wtedy następująco: .
Równanie spadku swobodnego wygląda wtedy następująco: 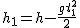 , ale człon , ale człon 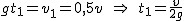 , zatem , zatem 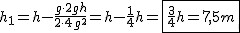 . .
§ 2. Rzut pionowy w górę
2.1. Równania ruchu
Równanie rzutu pionowego w górę jest analogiczne do ruchu jednostajnie opóźnionego z prędkością początkową (patrz linkowany temat).
Równania ruchu w rzucie pionowym w górę
znak "-" bo oś Oy jest skierowana do góry (patrz oznaczenia).
2.2. Czas spadku
Tak jak poprzednim razem postaram się pokazać jaki jest czas spadku na dowolną wysokość.
Czas spadku na dowolną wysokość w rzucie pionowym w górę (rozwiązanie ogólne)
Zauważmy, że nie możemy powiedzieć nic konkretnego o znaku przed pierwiastkiem. Wszak rozważaliśmy przypadek najogólniejszy. Przeanalizujmy przypadki łatwiejsze.
Gdy ciało spada na poziom  : :
Tutaj nie możemy zajmować się wyrażenie ze znakiem "-" przed pierwiastkiem, gdyż wartość pierwiastka jest zawsze większa od 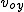 . Gdybyśmy założyli, że wzór z minusem jest do przyjęcia, to otrzymalibyśmy . Gdybyśmy założyli, że wzór z minusem jest do przyjęcia, to otrzymalibyśmy 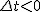 , a my analizowaliśmy ruch od momentu , a my analizowaliśmy ruch od momentu  , zatem takie rozwiązanie nas nie interesuje.
Oraz gdy ciało zostaje wyrzucone z poziomu zerowego: , zatem takie rozwiązanie nas nie interesuje.
Oraz gdy ciało zostaje wyrzucone z poziomu zerowego:
Tutaj nie możemy pominąć żadnego rozwiązania, gdyż pierwiastek jest nie mniejszy niż  .
Nie rzadko proszą nas w zadaniach o podanie czasu, po jakim ciało znajdzie się ponownie na wysokości zerowej. Kiedy rozwiązaliśmy przypadek ogólny, nie pozostaje nic prostszego jak podstawić odpowiednie wielkości do rozwiązania ogólnego, tj. .
Nie rzadko proszą nas w zadaniach o podanie czasu, po jakim ciało znajdzie się ponownie na wysokości zerowej. Kiedy rozwiązaliśmy przypadek ogólny, nie pozostaje nic prostszego jak podstawić odpowiednie wielkości do rozwiązania ogólnego, tj. 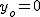 i i  : :
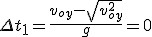
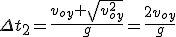
Rozwiązanie 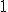 odpowiada sytuacji początkowej, kiedy wyrzucamy ciało z poziomu zerowego. Rozwiązanie odpowiada sytuacji początkowej, kiedy wyrzucamy ciało z poziomu zerowego. Rozwiązanie  jest całkowitym czasem ruchu ciała. Zauważmy, że połowa czasu spadania jest równa tzw. czasowi wznoszenia, który definiuje się jako rozwiązanie równania jest całkowitym czasem ruchu ciała. Zauważmy, że połowa czasu spadania jest równa tzw. czasowi wznoszenia, który definiuje się jako rozwiązanie równania  . Odpowiada ono sytuacji gdy ciało ma zerową prędkość, czy znajduje się na wysokości maksymalnej. Doszliśmy zatem do tego, że w jednorodnym polu grawitacyjnym czas wznoszenia na pewną wysokość jest równy czasowi spadku z tej wysokości. To właśnie jednorodność pola zapewnia nam prawdziwość powyższego stwierdzenia.
2.3. Wysokość maksymalna
Na wysokości maksymalnej prędkość ma wartość zerową zatem . Odpowiada ono sytuacji gdy ciało ma zerową prędkość, czy znajduje się na wysokości maksymalnej. Doszliśmy zatem do tego, że w jednorodnym polu grawitacyjnym czas wznoszenia na pewną wysokość jest równy czasowi spadku z tej wysokości. To właśnie jednorodność pola zapewnia nam prawdziwość powyższego stwierdzenia.
2.3. Wysokość maksymalna
Na wysokości maksymalnej prędkość ma wartość zerową zatem 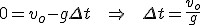 . Jest to czas po jakim ciało osiągnie wysokość maksymalną. Wstawmy to do równania ruchu . Jest to czas po jakim ciało osiągnie wysokość maksymalną. Wstawmy to do równania ruchu
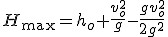 Wysokość maksymalna w rzucie pionowym w górę
Wysokość maksymalna w rzucie pionowym w górę
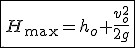
Przykład 2
Znaleźć prędkość początkową, z jaką wyrzucono ciało pionowo do góry, jeżeli na wysokości 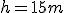 (licząc od punktu wyrzucenia ciała) znajdowało się ono dwukrotnie w odstępie czasu (licząc od punktu wyrzucenia ciała) znajdowało się ono dwukrotnie w odstępie czasu 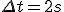 . . 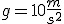 .
Rozwiązanie:
Przyjmijmy początek osi Oy w punkcie wyrzutu. Wtedy .
Rozwiązanie:
Przyjmijmy początek osi Oy w punkcie wyrzutu. Wtedy 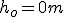 . Wiadomo, ze w jakimś momencie . Wiadomo, ze w jakimś momencie  ciało znalazło się na wysokości ciało znalazło się na wysokości 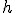 , a po czasie , a po czasie  znów znalazło się na tejże wysokości. Zatem nasze równania ruchu można zapisać znów znalazło się na tejże wysokości. Zatem nasze równania ruchu można zapisać
Po odjęciu od równania (2) równania (1) i podzieleniu przez 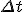 otrzymujemy równanie otrzymujemy równanie
Wstawmy ten czas do równania (1)
Wybrałem trudniejszą drogę dojścia do wyniku. Zadanie można rozwiązać w sposób o wiele prostszy dochodząc do wniosku, że po czasie t1+0,5Δt ciało osiąga wysokość maksymalną a następnie spada swobodnie z tej wysokości na wysokość h po upływie czasu 0,5Δt i tak naprawdę tylko to drugie równanie jest nam potrzebne bo z niego można bezpośrednio wyznaczyć prędkość początkową. Powodzenia!
§ 3. Rzut pionowy w dół
3.1. Równania ruchu
Równanie rzutu pionowego w górę jest analogiczne do ruchu jednostajnie przyspieszonego z prędkością początkową (patrz linkowany temat).
Równania ruchu w rzucie pionowym w dół
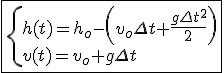
znak "-" ponieważ współrzędna wysokości cały czas się zmniejsza o podany nawias.
3.2. Czas spadku
Tak jak poprzednim razem postaram się pokazać jaki jest czas spadku na dowolną wysokość
Oczywiście wynik z minusem zostaje odrzucony, gdyż nie operujemy pojęciem ujemnego czasu.
Czas spadku w rzucie pionowym w dół
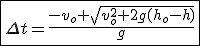
w szczególności gdy ciało spada na poziom 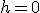
§ 4. Rzut poziomy
Rzut poziomy w polu grawitacyjnym jest superpozycją dwóch ruchów: jednostajnego w kierunku wyrzutu i jednostajnie przyspieszonego w dół. Niech ciał znajduje się na wysokości 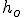 . Oś Oy jest skierowana w górę (g=[0,-g,0]) a oś Ox w prawo. Ciało rzucamy również w prawo z szybkością . Oś Oy jest skierowana w górę (g=[0,-g,0]) a oś Ox w prawo. Ciało rzucamy również w prawo z szybkością 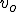 .
4.1. Równania ruchu .
4.1. Równania ruchu
Równania ruchu w rzucie poziomym
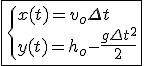
Wyznaczając czas z równania na  i wstawiając go do równania na i wstawiając go do równania na 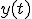 możemy uzyskać równanie toru po jakim porusza się rzucane ciało. Nie są to skomplikowane obliczenia, więc od razu napiszę wynik możemy uzyskać równanie toru po jakim porusza się rzucane ciało. Nie są to skomplikowane obliczenia, więc od razu napiszę wynik
Równanie toru w rzucie poziomym

Równanie to opisuje kawałek (gałąź) paraboli; kawałek, bo rozpatrujemy ruch od momentu x=0, zatem dziedziną tej funkcji jest  a zbiorem wartości a zbiorem wartości  .
4.2. Czas spadku
Znów rozpatrzymy czas spadku na dowolną wysokość. Sprawa jest identyczna jak w przypadku spadku swobodnego. Dlaczego? Wynika to z tego, że na czas spadku wpływa siła grawitacji, która działa tylko w pionie, zatem tylko ona decyduje o spadku ciała. To z jaką prędkością wyrzucimy ciało nie ma wpływu na czas spadku, bo na wyrzucone ciało w kierunku poziomym nie działa żadna siła (zakładamy brak sił oporu ośrodka).
Zatem czas na dowolną wysokość .
4.2. Czas spadku
Znów rozpatrzymy czas spadku na dowolną wysokość. Sprawa jest identyczna jak w przypadku spadku swobodnego. Dlaczego? Wynika to z tego, że na czas spadku wpływa siła grawitacji, która działa tylko w pionie, zatem tylko ona decyduje o spadku ciała. To z jaką prędkością wyrzucimy ciało nie ma wpływu na czas spadku, bo na wyrzucone ciało w kierunku poziomym nie działa żadna siła (zakładamy brak sił oporu ośrodka).
Zatem czas na dowolną wysokość 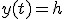 spadku wynosi spadku wynosi
Czas spadku w rzucie poziomym
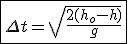
W szczególności gdy ciało spada na poziom 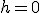
4.3. Zasięg
Zasięg to odległość w poziomie od miejsca wyrzutu ciała (x=0) do miejsca upadku (punkt (0,Z)). Zasięg tutaj będę oznaczał jako Z. Trzeba znaleźć moment, w którym y=0 i policzyć czas po jakim to nastąpi. Zrobiliśmy to w poprzednim podpunkcie: 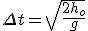 . Zasięg o nic innego jak . Zasięg o nic innego jak
Zasięg w rzucie poziomym

Przykład 3
Kula pistoletowa wystrzelona poziomo przebiła dwie poziomo ustawione kartki papieru w odległościach  i i 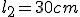 od pistoletu. Różnica wysokości na jakich znajdują się otwory w kartkach wynosi od pistoletu. Różnica wysokości na jakich znajdują się otwory w kartkach wynosi 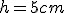 . Oblicz prędkość początkową kuli. . Oblicz prędkość początkową kuli.  Rozwiązanie:
Niewątpliwe założyć trzeba, ze kula nie traci swojej prędkości po zderzeniu z kartkami papieru. Niech w chwili
Rozwiązanie:
Niewątpliwe założyć trzeba, ze kula nie traci swojej prędkości po zderzeniu z kartkami papieru. Niech w chwili 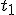 kula przebija pierwszą kartkę a w chwili kula przebija pierwszą kartkę a w chwili 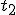 drugą. Wtedy drugą. Wtedy  i i 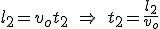 . Wiadomo, że w chwili . Wiadomo, że w chwili 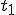 ciało znajduje się na wysokości ciało znajduje się na wysokości 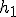 a w chwili a w chwili 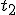 na wysokości na wysokości  , zatem , zatem
 i i 
Nie musimy znać wysokości początkowej, gdyż odległość w pionie między otworami to nic innego jak
Wstawiając wcześniej wyliczone czasy
§ 5. Rzut ukośny
Rzut ukośny jest superpozycją ruchów: jednostajnego w kierunku wyrzutu ciała i rzutu pionowego w górę w pionie rzecz jasna. Niech oś Oy będzie skierowana w górę a oś Ox w prawo. W chwili początkowej ciało znajduje się w punkcie (0,0) i nadajemy mu prędkość 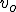 skierowaną pod kątem skierowaną pod kątem  to poziomu (osi Ox).
5.1. Równanie ruchu
Najpierw trzeba rozłożyć prędkość to poziomu (osi Ox).
5.1. Równanie ruchu
Najpierw trzeba rozłożyć prędkość 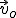 na dwie składowe: wzdłuż osi Ox na dwie składowe: wzdłuż osi Ox 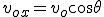 i wzdłuż osi Oy i wzdłuż osi Oy 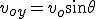 , zatem , zatem
Równania ruchu w rzucie ukośnym

I postępując tak jak w przypadku rzutu poziomego wyznaczamy tor ruchu ciała
Równanie toru w rzucie ukośnym

Równanie to opisuje pewną funkcję kwadratową, której dziedziną jest 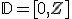 a zbiorem wartości a zbiorem wartości 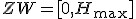 .
5.2. Czas wznoszenia
Analizując ten sam podpunkt z rzutu poziomego, można dojść do wniosku, że czas wznoszenia na dowolną wysokość .
5.2. Czas wznoszenia
Analizując ten sam podpunkt z rzutu poziomego, można dojść do wniosku, że czas wznoszenia na dowolną wysokość  , to rozwiązanie równania , to rozwiązanie równania
Czas wznoszenia w rzucie ukośnym
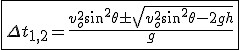
Oczywiście bierzemy pod uwagę oba czasy bo ciało dwa razy znajduje się na jeden wysokości. W szczególności gdy 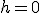
 - dotyczy sytuacji początkowej - dotyczy sytuacji początkowej
 - to czas po jakim od momentu wyrzucenia ciała, ono ponownie znajdzie się na wysokości 0 - to czas po jakim od momentu wyrzucenia ciała, ono ponownie znajdzie się na wysokości 0
Zatem znając ten czas możemy obliczyć zasięg w rzucie ukośnym, czego dotyczy następny podpunkt.
5.3. Zasięg
Posileni wiedzą z punku traktującego o rzucie ukośnym możemy przejść od razu do równań
Z równości  wnioskujemy, że wnioskujemy, że 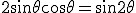 , zatem , zatem
Zasięg w rzucie ukośnym
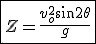
Kiedy zasięg jest największy? Kiedy sinus kąta ma największą wartość, którą jest 1. Rozpatrujemy kąty z przedziały 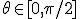 . Sinus kąta prostego ma największą wartość zatem . Sinus kąta prostego ma największą wartość zatem 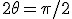 czyli czyli  , a więc największy zasięg otrzymamy gdy rzucimy coś pod kątem 45°. Możemy zapisać , a więc największy zasięg otrzymamy gdy rzucimy coś pod kątem 45°. Możemy zapisać
5.4. Wysokość maksymalna
Nasz rzut w pionie opisują równania
Ciało na wysokości maksymalnej ma zerową składową prędkości y-kowej, zatem 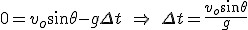 . Wstawiamy to teraz do równania na . Wstawiamy to teraz do równania na 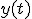
Wysokość maksymalna w rzucie ukośnym
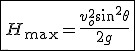
Przykład 4
Pod jakim kątem do poziomu wyrzucono ciało, jeżeli wiadomo, że maksymalna wysokość, na jaką wzniosło się ciało jest cztery razy mniejsza od zasięgu rzutu?
Rozwiązanie:
Korzystamy z wcześniej wyprowadzonych wzorów: 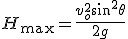 oraz oraz 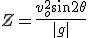 . Wiemy, że . Wiemy, że 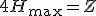 , zatem , zatem
Działamy tylko na kątach ostrych, a w takowych istnieje tylko jeden kąt, którego sinus i cosinus przyjmują takie same wartości
|
 |
|
|