 |
 |
 |
    |
|
Szybkość średnia
Szybkość średnia
Zdecydowałem się na pominięcie pojęcia prędkości średniej, która jest zdefiniowana jako wektor 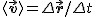 . Jak widać, jeśli . Jak widać, jeśli 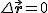 , to prędkość średnia znika. Taka sytuacja ma miejsce na przykład wówczas gdy jedziemy do pewnego miejsca, a potem wracamy do punktu wyjścia. W przytłaczającej większości przypadków interesuje nas średnia wartość prędkości na tej drodze, czyli szybkość średnia. Dlatego ograniczę się do policzenia przykładu wykorzystującego prędkość średnią. , to prędkość średnia znika. Taka sytuacja ma miejsce na przykład wówczas gdy jedziemy do pewnego miejsca, a potem wracamy do punktu wyjścia. W przytłaczającej większości przypadków interesuje nas średnia wartość prędkości na tej drodze, czyli szybkość średnia. Dlatego ograniczę się do policzenia przykładu wykorzystującego prędkość średnią.
§ 1. Pojęcie szybkości średniej
Szybkość średnia jest to stosunek całkowitej drogi jaką pokonało ciało podczas ruchu do czasu trwania tego ruchu.
Szybkość jest stała bądź zmienia się w sposób zauważalny[1]
Szybkość nieustannie[2,3] się zmienia
§ 2. Szybkość średnia w ruchu jednostajnym
Równanie ruchu jednostajnego wygląda następująco
Jeżeli  jest chwilą po jakiej kończy się mierzyć czas ruchu, to jest chwilą po jakiej kończy się mierzyć czas ruchu, to
Szybkość średnia w ruchu jednostajnym prostoliniowym
gdzie
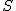 - całkowita droga przebyta przez ciało, - całkowita droga przebyta przez ciało,
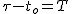 - całkowity czas trwania ruchu.
W ruchu jednostajnym szybkość jest stała, dlatego stanowi ona także szybkość średnią dla tego ruchu.
Jeżeli w różnych okresach ruchu ciało miało inne szybkości, to posłużyć się trzeba tzw. średnią arytmetyczną ważoną, gdzie wagami są okresu czasu. Pokazują to poniższe przykłady. - całkowity czas trwania ruchu.
W ruchu jednostajnym szybkość jest stała, dlatego stanowi ona także szybkość średnią dla tego ruchu.
Jeżeli w różnych okresach ruchu ciało miało inne szybkości, to posłużyć się trzeba tzw. średnią arytmetyczną ważoną, gdzie wagami są okresu czasu. Pokazują to poniższe przykłady.
Przykład 1
Przez pewien okres czasu  ciało poruszało się z szybkością ciało poruszało się z szybkością  a następnie w odstępie czasu a następnie w odstępie czasu  z szybkością z szybkością 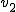 . Ile wynosi szybkość średnia podczas tego ruchu?
Rozwiązanie:
Droga przebyta w czasie . Ile wynosi szybkość średnia podczas tego ruchu?
Rozwiązanie:
Droga przebyta w czasie  : : 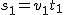 . Droga przebyta w czasie . Droga przebyta w czasie 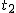 : : 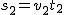 . Całkowita droga pokonana w czasie tego ruchu: . Całkowita droga pokonana w czasie tego ruchu: 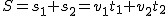 . Całkowity czas trwania tego ruchu: . Całkowity czas trwania tego ruchu:  . Szybkość średnia będzie zatem wynosić: . Szybkość średnia będzie zatem wynosić: 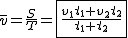 . Ta postać okazuje się być bardzo przydatna przy rozwiązywaniu zadań. . Ta postać okazuje się być bardzo przydatna przy rozwiązywaniu zadań.
Przykład 2
Ciało przez pierwszą połowę czasu porusza się z szybkością 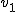 a pozostałą połowę czasu z szybkością a pozostałą połowę czasu z szybkością 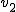 . Jaka jest szybkość średnia tego ciała podczas całego ruchu?
Rozwiązanie:
Korzystamy z powyższego wzoru: . Jaka jest szybkość średnia tego ciała podczas całego ruchu?
Rozwiązanie:
Korzystamy z powyższego wzoru:  . Wiemy, że . Wiemy, że 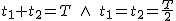 , zatem , zatem 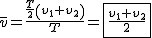 . .
Przykład 3
Ciało połowę całej drogi poruszało się z szybkością  a pozostałą połowę drogi z szybkością a pozostałą połowę drogi z szybkością 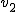 . Jaka jest szybkość średnia tego ciała podczas całego ruchu?
Rozwiązanie:
Korzystajmy z powyższego wzoru: . Jaka jest szybkość średnia tego ciała podczas całego ruchu?
Rozwiązanie:
Korzystajmy z powyższego wzoru:  . Wiemy, że . Wiemy, że  ,
zatem ,
zatem  . Tak więc . Tak więc 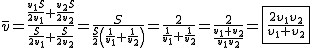 . .
Przykład 4
Rowerzysta jechał z miasta A do miasta B. Połowę drogi z A do B przejechał z szybkością 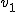 . Następnie przez pierwszą połowę pozostałego czasu podróży jechał z szybkością . Następnie przez pierwszą połowę pozostałego czasu podróży jechał z szybkością  , a w ciągu drugiej połowy tego czasu szedł pieszo z szybkością , a w ciągu drugiej połowy tego czasu szedł pieszo z szybkością  . Obliczyć szybkość średnią rowerzysty w tej podróży.
Rozwiązanie:
Należy nieco poszerzyć wzór na szybkość średnią . Obliczyć szybkość średnią rowerzysty w tej podróży.
Rozwiązanie:
Należy nieco poszerzyć wzór na szybkość średnią  . Niech całą drogą pokonaną przez rowerzystę będzie . Niech całą drogą pokonaną przez rowerzystę będzie  . Wiadomo, że . Wiadomo, że  , a także , a także 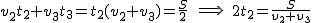 . Widać, że mianownik wzoru na szybkość średnią to po prostu . Widać, że mianownik wzoru na szybkość średnią to po prostu 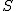 . .
 , zatem , zatem 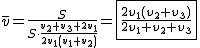
Przykład 5
Pociąg jedzie z praktycznie stałą prędkością 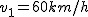 , najpierw dokładnie na wschód przez , najpierw dokładnie na wschód przez 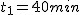 , następnie w kierunku północno-wschodnim pod kątem , następnie w kierunku północno-wschodnim pod kątem 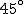 do poprzedniego przez do poprzedniego przez  , a w końcu na zachód przez , a w końcu na zachód przez 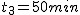 . Jaki jest średni wektor prędkości pociągu w czasie tego ruchu?
Rozwiązanie:
Żeby podać średni wektor prędkości należy podać jego wartość i kierunek, co można zrobić np. poprzez wyznaczenie kąta jaki tworzy szukany wektor z wybranym kierunkiem. Wybierzmy w tym celu układ współrzędnych tak, że kierunek wschodni pokrywa się z osią x a kierunek północny z osią y. Ponadto, niech początek naszego układu znajduje się w miejscu startu.
Rozbijmy nasze przemieszczenie na przemieszczenia w pionie i poziomie. Wówczas łatwo znajdziemy kat jaki tworzy wektor prędkości średniej z osią x: . Jaki jest średni wektor prędkości pociągu w czasie tego ruchu?
Rozwiązanie:
Żeby podać średni wektor prędkości należy podać jego wartość i kierunek, co można zrobić np. poprzez wyznaczenie kąta jaki tworzy szukany wektor z wybranym kierunkiem. Wybierzmy w tym celu układ współrzędnych tak, że kierunek wschodni pokrywa się z osią x a kierunek północny z osią y. Ponadto, niech początek naszego układu znajduje się w miejscu startu.
Rozbijmy nasze przemieszczenie na przemieszczenia w pionie i poziomie. Wówczas łatwo znajdziemy kat jaki tworzy wektor prędkości średniej z osią x:  . Policzę teraz przemieszczenia pociągu w kolejnych przedziałach czasu (patrz treść zadania). . Policzę teraz przemieszczenia pociągu w kolejnych przedziałach czasu (patrz treść zadania). 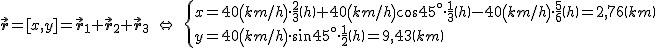 .
Zatem wartość przemieszczenia pociągu wynosi .
Zatem wartość przemieszczenia pociągu wynosi  . Tym samym wartość prędkości średniej jest równa . Tym samym wartość prędkości średniej jest równa  . A . A  . .
§ 3. Szybkość średnia w ruchu jednostajnie przyspieszonym
Równania ruchu jednostajnie przyspieszonego wyglądają następująco
Jeśli  będzie chwilą, w której kończymy pomiar ruchu, to będzie chwilą, w której kończymy pomiar ruchu, to
gdzie
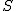 - całkowita droga przebyta przez ciało, - całkowita droga przebyta przez ciało,
 - całkowity czas trwania ruchu.
Z pierwszego równania wynika, że - całkowity czas trwania ruchu.
Z pierwszego równania wynika, że 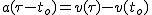 . Po podzieleniu równania drugiego przez . Po podzieleniu równania drugiego przez  otrzymujemy otrzymujemy
Szybkość średnia w ruchu jednostajnie przyspieszonym prostoliniowym
Ostatnie r-nie pokazuje, że szybkość średnia w ruchu jednostajnie przyspieszonym to średnia arytmetyczna szybkości końcowej i początkowej.
[1] Poprzez pojęcie zauważalny rozumiem ruch, w którym szybkość nie zmienia się w sposób ciągły, tzn. w przedziale czasu 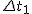 ciało ma szybkość ciało ma szybkość 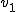 , w przedziale czasu , w przedziale czasu 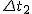 ma szybkość ma szybkość  itd. Definicje szybkości średniej podane przeze mnie odnoszą się tylko do składowej x-owej. Analogiczne zależności obowiązują dla pozostałych składowych.
[2] Tutaj z kolei przez słowo nieustannie rozumiem ruch, w którym szybkość zmienia się w sposób ciągły, tzn. przedziały czasu, w których szybkość można uważać za stałą dążą do zera ( itd. Definicje szybkości średniej podane przeze mnie odnoszą się tylko do składowej x-owej. Analogiczne zależności obowiązują dla pozostałych składowych.
[2] Tutaj z kolei przez słowo nieustannie rozumiem ruch, w którym szybkość zmienia się w sposób ciągły, tzn. przedziały czasu, w których szybkość można uważać za stałą dążą do zera ( ).
[3] Wartość średnią danej wielkości można notować na kilka sposobów: ).
[3] Wartość średnią danej wielkości można notować na kilka sposobów:  , ,  lub lub  . Pierwsze oznaczenie jest najczęściej stosowanym przez fizyków; dla matematyków "kreska nad symbolem" . Pierwsze oznaczenie jest najczęściej stosowanym przez fizyków; dla matematyków "kreska nad symbolem" 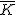 oznacza najczęściej liczbę sprzężoną do liczby zespolonej oznacza najczęściej liczbę sprzężoną do liczby zespolonej 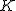 . .
|
 |
|
|