|
Transformacja Galileusza
Transformacja Galileusza
Transformacja lub inaczej przekształcenie Galileusza jest to przekształcenie wiążące położenie pewnego punktu P w dwóch układach inercjalnych S oraz S'.
§ 1. Układ inercjalny
Układ inercjalny to taki układ, w którym wszystkie prawa fizyczne występują w "standardowej" postaci. Układ taki pozostaje w spoczynku bądź porusza się postępowym ruchem jednostajnym prostoliniowym (bez obrotów) gdy nie działają nań żadne siły zewnętrzne. Układ ten nazywa się układem inercjalnym gdyż obowiązuje w nim I zasada dynamiki - zasada bezwładności; (inercja znaczy m. in. bezwładność). Każdy układ poruszający się postępowym ruchem jednostajnym prostoliniowym (bez obrotów) względem układu inercjalnego jest także układem inercjalnym. Pogrubioną część można traktować jako twierdzenie, które zostanie wkrótce dowiedzione.
§ 2. Matematyczna postać transformacji Galileusza
Z zamieszczonego rysunku widać, że  . Załóżmy, że układ S' porusza się ze stałą prędkością translacyjną . Załóżmy, że układ S' porusza się ze stałą prędkością translacyjną 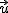 względem układu nieruchomego jakim jest układ inercjalny S.
Rozpatrzmy ruch początku układu współrzędnych S' względem początku układu S w przedziale czasu względem układu nieruchomego jakim jest układ inercjalny S.
Rozpatrzmy ruch początku układu współrzędnych S' względem początku układu S w przedziale czasu 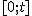 . Można wykazać (porównaj to równanie z r-niem ruchu jednostajnego prostoliniowego Ruchy prostoliniowe), że . Można wykazać (porównaj to równanie z r-niem ruchu jednostajnego prostoliniowego Ruchy prostoliniowe), że
Podstawmy 
Jeśli założymy, że w chwili  początki układów pokrywały się, tj. początki układów pokrywały się, tj. 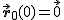 , to otrzymamy
Matematyczna postać transformacji Galileusza , to otrzymamy
Matematyczna postać transformacji Galileusza
§ 3. Konsekwencje wynikające z transformacji Galileusza
Przepiszmy transformację Galileusza w następującej postaci
Jeśli rozpatrzymy nasze układy po czasie  to to 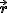 i i 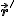 zmienią się do odpowiednio zmienią się do odpowiednio 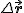 i i 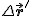 , zatem po tym czasie nasza transformacja będzie postaci , zatem po tym czasie nasza transformacja będzie postaci
Po podzieleniu przez  otrzymamy
Klasyczne prawo składania prędkości otrzymamy
Klasyczne prawo składania prędkości
 - prędkość punktu P w układzie S, - prędkość punktu P w układzie S,
 - prędkość punktu P w układzie S', - prędkość punktu P w układzie S',
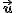 - prędkość układu S' względem S - tzw. prędkość unoszenia.
Przypomnijmy nasze założenie: - prędkość układu S' względem S - tzw. prędkość unoszenia.
Przypomnijmy nasze założenie:  , i sprawdźmy co z niego wynika. Rozpatrzmy ponownie układy po czasie , i sprawdźmy co z niego wynika. Rozpatrzmy ponownie układy po czasie  . Prędkości . Prędkości 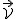 i i 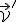 zmieniły się do odpowiednio zmieniły się do odpowiednio 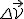 i i  natomiast natomiast  . Zatem nasze klasyczne prawo składania prędkości wygląda następująco . Zatem nasze klasyczne prawo składania prędkości wygląda następująco
Tak jak ostatnio, po podzieleniu przez 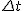 mamy, że mamy, że
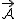 - to przyspieszenie punktu P w układzie S, - to przyspieszenie punktu P w układzie S,
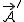 - to przyspieszenie punktu P w układzie S'.
Co na podstawie 2. zasady dynamiki możemy wyrazić jako
Niezmienność praw fizycznych względem układów inercjalnych - to przyspieszenie punktu P w układzie S'.
Co na podstawie 2. zasady dynamiki możemy wyrazić jako
Niezmienność praw fizycznych względem układów inercjalnych
Zatem układ poruszający się ze stałą prędkością translacyjną po linii prostej względem układu inercjalnego także jest układem inercjalnym, gdyż wszystkie prawa pozostają w nim w "standardowej" postaci. Zatem pogrubione wyżej twierdzenie zostało dowiedzione.
Przykład 1 - zadanie maturalne
Przeprawa promowa ludzi i samochodów odbywa się na rzece o szerokości 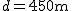 . Prędkość własna promu wynosi . Prędkość własna promu wynosi  i jest skierowana prostopadle do brzegu rzeki. Prędkość nurtu rzeki wynosi i jest skierowana prostopadle do brzegu rzeki. Prędkość nurtu rzeki wynosi 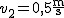 . Oblicz prędkość promu względem brzegu rzeki oraz czas, jaki zajmie mu jej przepłynięcie.
Rozwiązanie:
Z punktu widzenia obserwatora będącego na brzegu rzeki prędkość w jego układzie to . Oblicz prędkość promu względem brzegu rzeki oraz czas, jaki zajmie mu jej przepłynięcie.
Rozwiązanie:
Z punktu widzenia obserwatora będącego na brzegu rzeki prędkość w jego układzie to 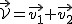 a wartość tej prędkości można policzyć z twierdzenia Pitagorasa a wartość tej prędkości można policzyć z twierdzenia Pitagorasa  .
Składowa prędkości nurtu rzeki nie wpływa na długość przepływu promu. Czas zależy od prędkości własnej promu, zatem .
Składowa prędkości nurtu rzeki nie wpływa na długość przepływu promu. Czas zależy od prędkości własnej promu, zatem 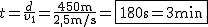 . .
Przykład 2 - zadanie maturalne
Kajakarz przepływa rzekę o szerokości  po najkrótszej drodze w ciągu po najkrótszej drodze w ciągu 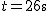 . Prędkość prądu rzeki . Prędkość prądu rzeki 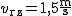 .
a) oblicz tangens kąta pod jakim należy ustawić oś kajak do brzegu rzeki, aby przepłynął ją po najkrótszej drodze.
b) Oblicz wartość prędkości .
a) oblicz tangens kąta pod jakim należy ustawić oś kajak do brzegu rzeki, aby przepłynął ją po najkrótszej drodze.
b) Oblicz wartość prędkości  jaką kajakowi nadaje wioślarz.
Rozwiązanie:
Najkrótsza droga w tym wypadku to linia prostopadła do brzegów rzeki. Rzeczą naturalną jest, że wioślarz musi płynąć pod pewnym kątem przeciwnie do kierunku nurtu rzeki, aby utrzymać kierunek prostopadły. Biorąc pod uwagę dwie pierwsze dane można obliczyć składową prędkości prostopadłą do brzegów rzeki jaką kajakowi nadaje wioślarz.
Rozwiązanie:
Najkrótsza droga w tym wypadku to linia prostopadła do brzegów rzeki. Rzeczą naturalną jest, że wioślarz musi płynąć pod pewnym kątem przeciwnie do kierunku nurtu rzeki, aby utrzymać kierunek prostopadły. Biorąc pod uwagę dwie pierwsze dane można obliczyć składową prędkości prostopadłą do brzegów rzeki  . Tangens kąta . Tangens kąta  . Wartość prędkości wioślarza to . Wartość prędkości wioślarza to 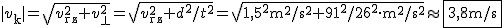
Dodatek
Transformacja Galileusza metodą różniczkowania.
Wychodzimy z tego samego równania wiążącego położenie punktu P w dwóch układach inercjalnych
Przepiszmy to tak jak poprzednio 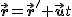 . Teraz wystarczy dwa razy zróżniczkować całość po czasie
Klasyczne prawo składania prędkości . Teraz wystarczy dwa razy zróżniczkować całość po czasie
Klasyczne prawo składania prędkości
Jeszcze jedno różniczkowanie i po pomnożeniu obustronnym przez masę bezwładną
Czyli to co wcześniej - niezmienność praw fizycznych w układach poruszających względem siebie ruchem jednostajnym prostoliniowym.
|