 |
 |
 |
    |
|
Zasady dynamiki Newtona
Zasady dynamiki Newtona
Isaac Newton swoje trzy prawa ruchu wysnuł z obserwacji swoich jak i Galileusza. Prawa te w oryginale noszą nazwę Axiomata sive leges motus i zawarte zostały w dziele Newtona Philosophiae Naturalis Principia Mathematica z 1687 roku. Te postulaty wprowadziły dwa nowe pojęcia: masy i siły. Nie istnieją formalne definicje tych pojęć, ale podejmuje się próby stworzenia tzw. definicji operacyjnych. Tutaj proponuję nie definiować siły za pomocą II zasady dynamiki, gdyż jak zdefiniować np. siłę nacisku za pomocą tej definicji?
§ 0. Definicje intuicyjne podstawowych pojęć
Bezwładność jest to zdolność ciał do przeciwstawiania się wszelkim zmianom ruchu. Masa bezwładna jest miarą bezwładności, czyli tego jak trudno zmienić ruch ciała. Siła jest miarą oddziaływań między ciałami.. Z ostatniej definicji tej wynika wprost, że źródłem siły działającej na jakieś ciało jest drugie ciało.
§ 1. Treść zasad dynamiki Newtona
Zasady dynamiki Newtona
I zasada dynamiki (zasada bezwładności)
Jeżeli na ciało nie działają żadne, bądź siły które się równoważą to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.
II zasada dynamiki
Jeżeli siły działające na ciało nie równoważą się (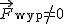 ), to ciało porusza się z przyspieszeniem wprost proporcjonalnym do przyłożonej siły wypadkowej ), to ciało porusza się z przyspieszeniem wprost proporcjonalnym do przyłożonej siły wypadkowej 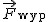 i jest skierowane tak samo jak siła wypadkowa doń przyłożona: i jest skierowane tak samo jak siła wypadkowa doń przyłożona:  .
III zasada dynamiki (akcji i reakcji)
Jeżeli ciało 1 działa na ciało 2 siłą .
III zasada dynamiki (akcji i reakcji)
Jeżeli ciało 1 działa na ciało 2 siłą  , to ciało 2 zawsze działa na ciało 1 siłą reakcji , to ciało 2 zawsze działa na ciało 1 siłą reakcji 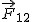 , przy czym , przy czym 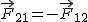 . .
§ 2. Znaczenie zasad dynamiki Newtona
Co te zasady dynamiki tak naprawdę oznaczają? Mogłoby się przecież wydawać, że I zasada dynamiki wynika z II; skoro 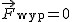 , to przyspieszenie też jest zerowe, więc ciało nie przyspiesza; a zatem albo porusza się ruchem jednostajnym prostoliniowym albo (jeśli wcześniej było w spoczynku) pozostaje w spoczynku. Dlatego wielu pewnie zadaje sobie pytanie - po co ta I zasada dynamiki?
2.1. I zasada dynamiki
Ma ona inne zadanie. Postuluje ona istnienie pewnego układu odniesienia. I zasadę bezwładności można sformułować następująco: , to przyspieszenie też jest zerowe, więc ciało nie przyspiesza; a zatem albo porusza się ruchem jednostajnym prostoliniowym albo (jeśli wcześniej było w spoczynku) pozostaje w spoczynku. Dlatego wielu pewnie zadaje sobie pytanie - po co ta I zasada dynamiki?
2.1. I zasada dynamiki
Ma ona inne zadanie. Postuluje ona istnienie pewnego układu odniesienia. I zasadę bezwładności można sformułować następująco:
Istnieje układ odniesienia, w którym ciało porusza się jednostajnie i prostoliniowo, jeżeli wszystkie nań działające siły się równoważą bądź gdy żadna siła nań nie działa.
Zatem I zasada dynamiki służy do wyróżnienia takiego układu, który nazywa się układem inercjalnym. Można też jej rolę przedstawić trochę inaczej: służy do podziału wszystkich układów odniesienia: na te spełniające I zasadę dynamiki - nazywane będą układami inercjalnymi - i te nie spełniające I zasady dynamiki układami nieinercjalnymi.
Każdy układ inercjalny to układ spoczywający bądź poruszający się ruchem jednostajnym prostoliniowym (bez przyspieszenia i obrotów) względem innego układu inercjalnego.
Układ nieinercjalny to układ odniesienia, który porusza się ruchem przyspieszonym lub/i wykonuje obroty względem inercjalnego układu odniesienia.
Jeżeli już wyróżniliśmy układ, w którym obowiązuje zasada bezwładności, to dopiero teraz możemy przejść do II zasady dynamiki, gdyż w powyższej postaci jest ona spełniona tylko w układach inercjalnych. Dlatego potrzebna jest I zasada dynamiki, gdyż bez niej nie można mówić o II zasadzie.
Zasada bezwładności obowiązuje także przy prędkościach bliskich c, pod warunkiem, że te prędkości są stałe.
2.2. II zasada dynamiki
Teraz możemy przejść do najbardziej praktycznej z zasad dynamiki. Mając daną siłę działającą na ciało i parametry początkowe tegoż ciała (x(0), v(0)) o ruchu ciała można powiedzieć wszystko, a to za sprawą właśnie II zasady dynamiki. Jej postać matematyczna jest często nazywana równaniami Newtona. Postać 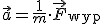 nie jest jednak w pełni ścisłą postacią II zasady dynamiki. Owszem, w ujęciu klasycznym masa nie zmienia się, więc postać ta jest dopuszczalna. Jednakże w pełni poprawnie II zasadę dynamiki opisuje zależność nie jest jednak w pełni ścisłą postacią II zasady dynamiki. Owszem, w ujęciu klasycznym masa nie zmienia się, więc postać ta jest dopuszczalna. Jednakże w pełni poprawnie II zasadę dynamiki opisuje zależność 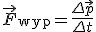 , dlatego to równanie nosi nazwę uogólnionej II zasady dynamiki. Postać tę można łatwo wyprowadzić w miejsce a dając Δv/Δt jednocześnie zauważając, że gdy masa jest stała to mΔv=Δp. Zatem przy stałej masie układu obie definicje są sobie równoważne.
II zasada dynamiki obowiązuje także dla prędkości bliskich c, ale tylko w uogólnionej postaci, gdyż wówczas nie można zaniedbać efektów relatywistycznych - zwiększania się masy bezwładnej. Zatem w mechanice relatywistycznej , dlatego to równanie nosi nazwę uogólnionej II zasady dynamiki. Postać tę można łatwo wyprowadzić w miejsce a dając Δv/Δt jednocześnie zauważając, że gdy masa jest stała to mΔv=Δp. Zatem przy stałej masie układu obie definicje są sobie równoważne.
II zasada dynamiki obowiązuje także dla prędkości bliskich c, ale tylko w uogólnionej postaci, gdyż wówczas nie można zaniedbać efektów relatywistycznych - zwiększania się masy bezwładnej. Zatem w mechanice relatywistycznej 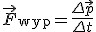 2.3. III zasada dynamiki
III zasada dynamiki nie zajmuje się badaniem ruchu ciała, ale czymś zupełnie innym. Logiczne jest, że gdy pchamy ścianę to ta na nas także musi oddziaływać, bo jeśli by nie reagowała na naszą siłę, to z pewnością leżelibyśmy już na ziemi. Jednakże czy ktoś mógł sobie zdawać sprawę o tym, ze te siły mają tę samą wartość? Zwrócić trzeba uwagę na to, że siły z III zasady dynamiki nie równoważą się, gdyż są przyłożone do do różnych ciał. Ta zasada dynamiki pełni poważna rolę w makroskopowym opisie zderzeń. To właśnie z tej zasady wynika zasada zachowania pędu (można to wykazać w pełni ściśle używając troszkę wyższej matematyki). Można powiedzieć więcej: III zasada dynamiki i zasada zachowania pędu są sobie nawzajem równoważne.
III zasadę dynamiki można spokojnie stosować, ale tylko w mechanice klasycznej, gdyż zasada ta mówi o tym, ze reakcja na akcję następuje błyskawicznie, co jest w konflikcie z STW, ponieważ tam największą prędkością przekazu informacji w przyrodzie jest skończona prędkość światła.
2.3. III zasada dynamiki
III zasada dynamiki nie zajmuje się badaniem ruchu ciała, ale czymś zupełnie innym. Logiczne jest, że gdy pchamy ścianę to ta na nas także musi oddziaływać, bo jeśli by nie reagowała na naszą siłę, to z pewnością leżelibyśmy już na ziemi. Jednakże czy ktoś mógł sobie zdawać sprawę o tym, ze te siły mają tę samą wartość? Zwrócić trzeba uwagę na to, że siły z III zasady dynamiki nie równoważą się, gdyż są przyłożone do do różnych ciał. Ta zasada dynamiki pełni poważna rolę w makroskopowym opisie zderzeń. To właśnie z tej zasady wynika zasada zachowania pędu (można to wykazać w pełni ściśle używając troszkę wyższej matematyki). Można powiedzieć więcej: III zasada dynamiki i zasada zachowania pędu są sobie nawzajem równoważne.
III zasadę dynamiki można spokojnie stosować, ale tylko w mechanice klasycznej, gdyż zasada ta mówi o tym, ze reakcja na akcję następuje błyskawicznie, co jest w konflikcie z STW, ponieważ tam największą prędkością przekazu informacji w przyrodzie jest skończona prędkość światła.
Przykład 1
Piłka ping-pongowa spada z wysokości 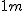 na stół i po odbiciu się wznosi się na wysokość na stół i po odbiciu się wznosi się na wysokość 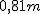 . Jaką wartość ma średnie przyspieszenie piłki w czasie . Jaką wartość ma średnie przyspieszenie piłki w czasie 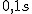 , w którym to czasie styka się ona ze stołem. Przyjąć kierunek spadania piłki za dodatni.
Rozwiązanie:
Należy skorzystać z uogólnionej II zasady dynamiki jak i ze zwykłej jej postaci: , w którym to czasie styka się ona ze stołem. Przyjąć kierunek spadania piłki za dodatni.
Rozwiązanie:
Należy skorzystać z uogólnionej II zasady dynamiki jak i ze zwykłej jej postaci: 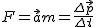 . U nas: . U nas: 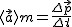 . Nie mamy tylko zmiany pędu. (Liczę na to, że masa się gdzieś skróci)
1° Spadek z wysokości . Nie mamy tylko zmiany pędu. (Liczę na to, że masa się gdzieś skróci)
1° Spadek z wysokości  . Skorzystam z tego, że ciało spadające z wysokości . Skorzystam z tego, że ciało spadające z wysokości 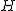 na stół uzyskuje prędkość na stół uzyskuje prędkość  (patrz: Rzuty w polu grawitacyjnym). Wyliczyłem prędkość z jaką kulka uderzy w stół.
2° Ruch do góry: do wysokości (patrz: Rzuty w polu grawitacyjnym). Wyliczyłem prędkość z jaką kulka uderzy w stół.
2° Ruch do góry: do wysokości 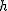 . Korzystam z tego, że czas wznoszenia na wysokość jest równy czasowi spadku z tej wysokości, zatem tak jak poprzednio . Korzystam z tego, że czas wznoszenia na wysokość jest równy czasowi spadku z tej wysokości, zatem tak jak poprzednio  . Wyliczyłem prędkość z jaką kulka się odbije od stołu.
Teraz obliczmy zmianę pędu kulki. (Pęd stołu możemy pominąć ze względu na to, że prędkość stołu jest bardzo mała: . Wyliczyłem prędkość z jaką kulka się odbije od stołu.
Teraz obliczmy zmianę pędu kulki. (Pęd stołu możemy pominąć ze względu na to, że prędkość stołu jest bardzo mała:  ). Prędkości przy uderzeniu o stół i po odbiciu od niego są przeciwnie skierowane, zatem ). Prędkości przy uderzeniu o stół i po odbiciu od niego są przeciwnie skierowane, zatem 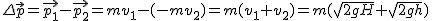 , czyli , czyli
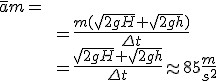
gdzie
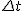 - to oczywiście czas zderzenia. - to oczywiście czas zderzenia.
Przykład 2
Człowiek stoi na wadze sprężynowej (dynamometrze), która wskazuje jego ciężar 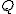 . Nad wagą jest zawieszony na dynamometrze ciężar . Nad wagą jest zawieszony na dynamometrze ciężar  .
1) Jakie siły będą wskazywać obydwa dynamometry, jeżeli człowiek zacznie pchać do góry rękami ciężar .
1) Jakie siły będą wskazywać obydwa dynamometry, jeżeli człowiek zacznie pchać do góry rękami ciężar 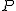 siłą siłą 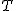 ?
2) Jaką siłę człowiek musi przyłożyć do ciężaru ?
2) Jaką siłę człowiek musi przyłożyć do ciężaru 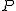 , aby górny dynamometr nic nie wskazywał?
3) jakie siły będą wskazywać obydwa dynamometry, jeżeli człowiek będzie ciągnął ciężar , aby górny dynamometr nic nie wskazywał?
3) jakie siły będą wskazywać obydwa dynamometry, jeżeli człowiek będzie ciągnął ciężar 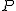 siłą siłą  w dół?
4) Jaką siłą człowiek musi ciągnąć ciężar w dół?
4) Jaką siłą człowiek musi ciągnąć ciężar  , aby dolny dynamometr nic nie wskazywał?
Rozwiązanie:
Całą sytuację chciałbym zanalizować bardzo szczegółowo z naciskiem na wykorzystanie zasad Newtona. Człowiek działa na wagę siłą nacisku N zatem waga działa na człowieka siłą reakcji R równą co do wartości N. Na człowiek działa jeszcze siła grawitacji Q. Faktem jest, że człowiek stoi nieruchomo zatem zgodnie z I zasadą dynamiki wszystkie siłą nań działające muszą się znosić. Na człowieka działają dwie siły: R i Q, zatem one się muszą równoważyć. Skoro R=Q i N=R to N=Q i to właśnie siłę N wskazuje początkowo dynamometr. Z dynamometrem na górze jest bardzo podobnie. Także wskazuje on ciężar ciała P.
1) Jeżeli człowiek zacznie pchać do góry ciężar P siłą T, to wskazanie dynamometru na górze zmniejszy o wartość T. Czyli górny wskaże wartość P-T. Natomiast zgodnie z III zasadą dynamiki, ciężar P działa na człowiek siłą T, zatem wskazanie dolnego dynamometru zwiększy się o T. Dolny pokaże Q+T.
2) Posileni poprzednim podpunktem widać, że siła ta musi być skierowana go góry i spełniać warunek P-T=0 zatem nasza siła T=P i taką siłę musimy przyłożyć do ciężaru na górze.
3) Sytuacja jest dokładnie odwrotna jak w 1). Ciągnąc w dół ciężar P zwiększamy wskazanie dynamometru górnego o T. Górny wskaże P+T. Znów korzystając z III zasady dynamiki dowiadujemy się, że ciężar P działa na nas siłą T zwróconą do góry (bo my działaliśmy w dół). Zatem dolny wskaże Q-T.
4) Tym razem skorzystamy z 3) podpunktu. Wiadomo, że siła musi być skierowana w dół i spełniać warunek Q-T=0 zatem T=Q i taką siłą musimy zadziałać. , aby dolny dynamometr nic nie wskazywał?
Rozwiązanie:
Całą sytuację chciałbym zanalizować bardzo szczegółowo z naciskiem na wykorzystanie zasad Newtona. Człowiek działa na wagę siłą nacisku N zatem waga działa na człowieka siłą reakcji R równą co do wartości N. Na człowiek działa jeszcze siła grawitacji Q. Faktem jest, że człowiek stoi nieruchomo zatem zgodnie z I zasadą dynamiki wszystkie siłą nań działające muszą się znosić. Na człowieka działają dwie siły: R i Q, zatem one się muszą równoważyć. Skoro R=Q i N=R to N=Q i to właśnie siłę N wskazuje początkowo dynamometr. Z dynamometrem na górze jest bardzo podobnie. Także wskazuje on ciężar ciała P.
1) Jeżeli człowiek zacznie pchać do góry ciężar P siłą T, to wskazanie dynamometru na górze zmniejszy o wartość T. Czyli górny wskaże wartość P-T. Natomiast zgodnie z III zasadą dynamiki, ciężar P działa na człowiek siłą T, zatem wskazanie dolnego dynamometru zwiększy się o T. Dolny pokaże Q+T.
2) Posileni poprzednim podpunktem widać, że siła ta musi być skierowana go góry i spełniać warunek P-T=0 zatem nasza siła T=P i taką siłę musimy przyłożyć do ciężaru na górze.
3) Sytuacja jest dokładnie odwrotna jak w 1). Ciągnąc w dół ciężar P zwiększamy wskazanie dynamometru górnego o T. Górny wskaże P+T. Znów korzystając z III zasady dynamiki dowiadujemy się, że ciężar P działa na nas siłą T zwróconą do góry (bo my działaliśmy w dół). Zatem dolny wskaże Q-T.
4) Tym razem skorzystamy z 3) podpunktu. Wiadomo, że siła musi być skierowana w dół i spełniać warunek Q-T=0 zatem T=Q i taką siłą musimy zadziałać.
Przykład 3
Za pomocą łańcuchów połączono 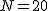 wagonów kolejowych, z których każdy ma masę wagonów kolejowych, z których każdy ma masę  . Wagony stoją na gładkim torze poziomym. Zbadać, który z sąsiednich wagonów można połączyć słabszym od innych łańcuchem, wytrzymującym co najwyżej . Wagony stoją na gładkim torze poziomym. Zbadać, który z sąsiednich wagonów można połączyć słabszym od innych łańcuchem, wytrzymującym co najwyżej  , jeżeli od strony lokomotywy podczas ruszania składu jest przyłożona siła , jeżeli od strony lokomotywy podczas ruszania składu jest przyłożona siła  Rozwiązanie:
Rozwiązanie:
Tak ja na zamieszczonym rysunku podzieliłem wagony na n i na N-n wagonów i zaznaczyłem siły naciągu dla każdych układów wagonów. Na układ N-n wagonów działa tylko siła T, a na układ n wagonów siła F-T. Cały układ ma jednakowe przyspieszenie a, zatem 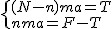 . Z pierwszego równania wyznaczę przyspieszenie . Z pierwszego równania wyznaczę przyspieszenie  i wstawiwszy to do drugiego równania i wstawiwszy to do drugiego równania  . Z warunków zadania, siła T musi spełniać warunek: . Z warunków zadania, siła T musi spełniać warunek: 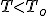 (interesuje nas mniejsza, a nie mniejsza lub równa wartość siły naciągu łańcucha. Chcemy znaleźć przecież miejsce gdzie możemy osłabić łańcuch), zatem (interesuje nas mniejsza, a nie mniejsza lub równa wartość siły naciągu łańcucha. Chcemy znaleźć przecież miejsce gdzie możemy osłabić łańcuch), zatem

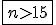 , ,
a więc począwszy od 16 wagonu możemy zastosować słabsze łańcuchy.
|
 |
|
|